Замечательные пределы. Первый замечательный предел

Первый замечательный предел.

Первый замечательный предел позволяет открывать неопределенность ().

Второй замечательный предел.

позволяет открыть неопределенность

Непрерывность функции. Классификация точек разрыва.

Функция f(x) называется непрерывной в точке , если выполняются следующие условия:

1)Функция определена в точке , т.е. существует f()

2)Существует конечный предел функции при x-> , т.е.

3)Этот предел равен значению функции в точке , т.е.

Функция называется непрерывной в точке 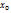б.м.в. приращению аргумента х этой точке соответствует бесконечно-малое п-риращение функции.

△x=x- – приращение аргумента

△y=y- – приращение функции

Классификация точек разрыва:

1)Точки разрыва первого рода (точки, в которых пределы слева и справа конечны, но друг другу не равны)

2)Точки разрыва второго рода. Точки, в которых хотя бы один из пределов слева или справа, равен бесконечности или не существует.

3)Точки устранимого режима – это точки, в разрыве которых предел функции существует(но не равен значению функции в этой точке).

К точкам устранимого разрыва относят к точкам разрыва первого рода.