Геометрический смысл производной

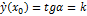
Производная функции в точке 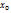равна угловому коэффициенту касательной, проведенной к графику функции в точке с абциссой

y- 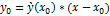– уравнение касательной.

Механический смысл производной.

Пусть материальная точка движется прямолинейно по закону S=f(t), предположим, что к моменту 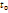точка прошла путь 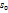, а к моменту времени t путь s, тогда за промежуток времени △t=t- 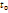материальная точка прошла путь △s=s- .

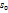V(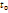)= 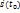Мех.смысл.пр-й: скорость прямолинейного движения материальной точки в данный момент времени есть производная от пути по времен, вычисленная в данный момент времени.

Основные правила дифференцирования.

1)(c)’=0

2)(x)=1

3)(U+V)’=U’+V’

4)(U*V)=U’*V+U*V’

4.1.(c*U)’=c*(U)’

4.2.(U*V*W)’=U’*V*W+V’*U*W+W’*U*V

5) ()’=

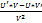
V≠0. U=U(x), V=V(x), W=W(x)

К 60 я хер знает вообще как вместить, это что-то вроде док-ва

(U+V)’=U’+V’

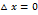
Зададим значению х приращение △x≠0, тогда функции U,V получат приращение △U,△V.

1)△y=(U+△U+V+△V)-(U+V)=△U+△V

2) =

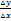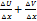
3)y’=

(U+V)’=U’+V’

Расстояние от точки до прямой