Эллипс. Каноническое уравнение эллипса. Исследование формы эллипса по его каноническому уравнению

1) Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F1 и F2, называемых фокусами эллипса, есть величина постоянная.

=2a – большая ось, a – большая полуось. 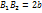-маленькая оси эллипса,b-малая полуось.

| |+| |=2a=const, 2a>2c, | |=2C – фокусное расстояние. 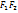-фокусы эллипса.

2) параметры эллипса–

Каноническое уравнение эллипс а.

3)a>b, . b>a,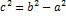

Первый вариант, как на рисунке, второй – вдоль оси Y.(оси не меняются)

Эксцентриситет эллипса. Связь эллипса с окружностью.

Эксцентриситет эллипса – это отношение расстояние между фокусами к длине большой оси.

1)a>b, Ɛ=

2)b>a, Ɛ=

0< Ɛ<1. a=b.

=1

Гипербола. Каноническое уравнение гиперболы. Исследование формы гиперболы по её уравнению.

где r и d не писать, линии, которые проходят через о;о – асимптоты.

Пусть на плоскости заданы две точки и и дано число a (0 < a < c). Гипербола - множество точек M плоскости, для каждой из которых модуль разности расстояний от точек и равен 2a. Точки и называются фокусами гиперболы; - действительная ось; - мнимая ось; O - центр; - левый и правый фокусы; - вершины.

– каноническое уравнение гиперболы.

Равнобочная гипербола 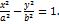(как на рисунке)

Сопряженная гипербола (ветви сверху и снизу)