2018-01-08
589
Точки: 1)Если функции f(x), φ(x), непрерывны в точке 
, то их сумма произведения и частное, при условии φ(
) 
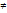0 также является непрерывными функциями.
2)Если функция f(x) непрерывна в точке 
>0, то существует такая определенность , в которой f(x)>0
3)Если функция f(u) непрерывна в точке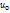 
, а функция u=φ(x) непрерывная в точке , то сложная функция f(u(x))
Отрезок:
1)Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
2)Если функция непрерывна, на отрезке, то она достигает наименьшего и наибольшего значения.
3)Если функция непрерывна на отрезка, а на концах отрезка значения функция противоположны по знаку, то внутри отрезка найдется такая точка, в которой функция равна нулю.
Приращения аргумента и функции. Производная. Схема вычисления производной.
△x=x- – приращение аргумента
△y=y- 
– приращение функции
Производной функции в точке называется предел отношения приращения функции приращению аргумента при условии, что приращение аргумента стремится к нулю.
Функция, имеющая производную в точке называется дифференцируемой в этой точке. Операция вычисления производной называется дифференцированием функции.
Схема вычисления производной.
1)△y(
)=y(
)-y()
2) 
3) 
