Домашний типовой расчет
по теме:
«Элементы математической статистики»
Выполнила ст. гр. ГНГ-10 Ларукова А.
Проверила Прудникова О. М.
Ухта 2012
Элементы математической статистики.
Задача
Выполнение задания
Известны х1 ,х2 ,…,хn – результаты независимых наблюдений над случайной величиной х.
Х – проходка на долото
13 вариант
| 136.6 | |||||||||
Сгруппируем эти данные в интегральную таблицу
а) Определить объем выборки
n = 76
б) Определить Х maxи Xmin элементы выборки
Хmax = 307 Xmin = 2
Тогда размах выборки - R = Хmax - Xmin =305
в) По формуле Серджеса определяем количество интервалов
k = 1+3,322∙lg(n) = 7,25 ≈ 7
г) Рассмотрим шаг разбиения
h = R÷k = 305÷7 = 43,57
д) Вычислим начальное значение интервальной таблицы
Xнач = Xmin -0,5∙h = -19,79
е) Составим интервальную таблицу
где Х – проходка на долото
| Xi - … | (-19,79;29,78) | (29,78;67,35) | (67,35;110,92) | (110,92;154,49) | (154,49;198,06) | (198,06;241,63) | (241,63;285,2) | (285,2;328,77) |
| ni | ||||||||
| Xi ср | 4,995 | 48,565 | 89,135 | 132,705 | 241,63 |
Построить полигон частот, гистограмму и эмпирическую функцию распределения.
а) Построение полигона частот
Полигоном частот – называют ломанную, отрезки которой соединяют точки (х1,n1), (х2,n2), (хk,nk). Для построения полигона на оси абсцисс откладывают варианты хi, а на оси ординат – соответствующе им частоты ni. Точки (хi, ni) соединяют отрезками прямых и получают полигон частот.
б) Построим гистограмму частот
Гистограммой частот – называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны отношению ni /n (плотность частоты).
в) Построить моду и медиану
Модой – называют варианту, которая имеет наибольшую частоту.
Медиана – называют варианту, которая делит вариационный ряд на две части, равные по числу вариант.
| Хi | (-19,79;29,78) | (29,78;67,35) | (67,35;110,92) | (110,92;154,49) | (154,49;328,77) |
| ni | |||||
| ni /h | 0,8 | 0,44 | 0,16 | 0,16 | 0,18 |
г) Найдем и построим эмпирическую функцию распределения
Эмпирической функцией распределения (функцией распределения выборки) – называют функцию F*(x) определяющую частоту события Х<х. F*(x) = nx /n

д) Построим кумуляту
Кумулята – это график составленный из накопительных частот то есть это сглаженное изображение эмпирической функции распределения.
| Хi | (-19,79;29,78) | (29,78;67,35) | (67,35;110,92) | (110,92;154,49) | (154,49;328,77) |
| ni | |||||
| ni /n | 35/76 | 19/76 | 7/76 | 7/76 | 8/76 |
| Xi ср | 4,995 | 48,565 | 89,135 | 132,705 | 241,63 |
Найдем несмещенную оценку математического ожидания и дисперсии случайной величины х
Х – проходка на долото
а) Несмещенная оценка

Xнесм = 
 =
= 

(Xвыб)2 =363,609


в) «Исправленное» среднее квадратическое отклонение.

 11691,37 = 11847,26
11691,37 = 11847,26

Найти интервальные оценки математического ожидания и дисперсии случайной величины х с надёжностью  = 0,9 и
= 0,9 и  = 0,95
= 0,95
X – проходка на долото; n = 76; Xвыб = 60,3; S = 108,85;  = 11691,37;
= 11691,37;  =
= 
а) Найдем интервальные оценки математического ожидания
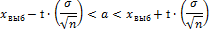
1) Ф(t) =  =
= 


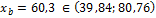
2) 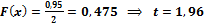



б) Найдем интервальные оценки дисперсии
1)  = 0,99; q(
= 0,99; q( ;n) = (0,99;76)
;n) = (0,99;76)


82,18  133,45
133,45

6753,55  17808,9
17808,9

 (6753,55;17808,9)
(6753,55;17808,9)
2)  = 0,95; q(
= 0,95; q( ;n) = (0,95;76)
;n) = (0,95;76)


89,91  126,37
126,37

8083,81  15969,38
15969,38

 (8083,81;15969,38)
(8083,81;15969,38)
Выдвинуть гипотезу об истинном значении параметра  нормального распределения и проверить ее при уровне значимости
нормального распределения и проверить ее при уровне значимости 
Выдвинем гипотезу об истинном значении параметра  нормального распределения и проверим ее при уровне значимости
нормального распределения и проверим ее при уровне значимости 

примем 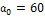
Проверим гипотенузу 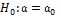
При конкурирующей гипотенузе 
Решение:
а) вычислим наблюдаемое значение критерия

б) при  найдем
найдем


нет основания отвергнуть гипотезу  ,т.е. выборочная средняя
,т.е. выборочная средняя  незначимо отличается от гипотетической (предполагаемой)генеральной средой
незначимо отличается от гипотетической (предполагаемой)генеральной средой 
Выдвинуть гипотезу о законе распределения случайной величины x проверить ее по критерию 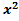 (Пирсона) при уровне значимости
(Пирсона) при уровне значимости 
Выведем гипотенузу о нормальном законе распределения случайной величины х и проверим ее по критерию 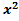 при уровне значимости
при уровне значимости  имеем
имеем 
 нормальный закон распределения наблюдается
нормальный закон распределения наблюдается
 нормальный закон распределения не наблюдается
нормальный закон распределения не наблюдается
а) Составим вспомогательную таблицу вида
| № | Частичный интервал 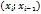 | Нормированный правый конец 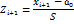 | Нормированный левый конец  |  |  | Теоретическая вероятность 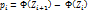 | Теоретическая частота  | Эмпирическая частота  |
| (-19,79; 29,78) | -0,28 | -0,74 | -0,1103 | -0,2703 | 0,16 | 12,16 | ||
| (29,78; 67,35) | 0,06 | -0,28 | 0,0239 | -0,1103 | 0,1342 | 10,2 | ||
| (67,35; 110,92) | 0,47 | 0,06 | 0,1808 | 0,0239 | 0,1569 | 11,92 | ||
| (110,92; 154,49) | 0,87 | 0,47 | 0,3078 | 0,1808 | 0,127 | 9,65 | ||
| (154,49; 328,77) | 2,47 | 0,87 | 0,4932 | 0,3078 | 0,1854 | 14,09 |
б) Сравним эмпирическую и теоретическую частоты.
эмпирическая частота  | |||||
теоретическая частота 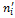 | 12,16 | 10,2 | 11,92 | 9,65 | 14,09 |
Вывод: расхождение случайно
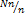 |  | 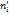 | 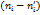 |  |  |
| 12,16 | 22,84 | 521,67 | 42,9 | ||
| 10,2 | 8,8 | 77,44 | 7,59 | ||
| 11,92 | -4,92 | 24,21 | 2,03 | ||
| 9,65 | -2,65 | 7,02 | 0,73 | ||
| 14,09 | -6,09 | 37,09 | 2,63 |
Задача
Применяя метод наименьших квадратов на основе экспериментальных данных найти эмпирическую формулу, выражающую зависимость y от x. Построить теоретическую зависимость и экспериментальные точки на одном графике.
| x | -2 | -1 | |||||
| y | 5,2 | 2,7 | -0,2 | -0,8 | -2,7 | -5,3 | -7,4 |
1) Для оценки вида функциональной зависимости представим данные таблицы на координатной плоскости.
Основываясь на график, можно предполагать, что данная функция зависимости является линейной 
2) Предусматриваем нахождения параметров ( этих зависимостей из условий минимума алгебраической суммы квадратического отклонения
этих зависимостей из условий минимума алгебраической суммы квадратического отклонения

3)Где коэффициенты 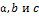 найдем из решения системы для квадратической зависимости:
найдем из решения системы для квадратической зависимости:

n-количество пар в таблице
4)Для решения системы следует составить вспомогательную таблицу
 |  |  |  |  |
| -2 | 5,2 | -10,4 | ||
| -1 | 2.7 | -2,7 | ||
| -0,2 | ||||
| -0,8 | -0,8 | |||
| -2,7 | -5,4 | |||
| -5,3 | -15,9 | |||
| -7,4 | -29,6 | |||
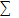 | -8,5 | -64,8 |
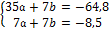















 0,0225;
0,0225;
Задача
При исследовании коэффициента трении полимерного волокна для двух образцов были получены следующие силы трения. Можно ли считать, что в среднем образцы одинаковы.
| 1 обр | 5,01 | 4,89 | 4,89 | 4,88 | 4,88 | 4,92 |
| 2 обр | 4,88 | 5,00 | 5,02 | 4,90 | 4,90 | 4,95 |


Ход решения: 1) Вычислить 

Задача 3
Известны результаты наблюдений за свойствами горных пород, Р0 – предел текучести по штампу, Рш – твердость по штампу.
1) Исследовать, принадлежат ли минимальные и максимальные члены выборок к основной генеральной совокупности по правилу трех сигм и критерию Стьюдента.
2) Найти несмещенные оценки математического ожидания и дисперсии Р0 и Рш.
3) Найти коэффициенты корреляции между Р0 и Рш.
4) Получить уравнение линейной регрессии Рш на Р0.
5) Проверить гипотезу о значимости коэффициента корреляции при условии значимости α = 0,05
Известны результаты наблюдений за свойствами горных пород, которые приведены в таблице.
| Р0 | |||||||||
| Рш | |||||||||
| Р0 | |||||||||
| Рш |
где Р0 - предел текучести по штампу, Рш - твердость по штампу
1) Составим вспомогательную расчетную таблицу
Примем Р0 за xi и Рш за yi.
| № | xi | yi | xi2 | yi2 | xi yi |
 |
Из таблицы получили:
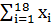 = 2451
= 2451
 =1181
=1181
 =374249
=374249
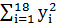 =85171
=85171
 =173725
=173725
Рассчитаем математическое ожидание:
 =
=  = 2451/17 = 144,18
= 2451/17 = 144,18
 =
=  = 1181/17 =69,47
= 1181/17 =69,47
Рассчитаем дисперсию:
σx2 =  2 = 22014,65 – 20770,57 = 1244,08
2 = 22014,65 – 20770,57 = 1244,08
σy2 =  2 = 5010,06 – 4826,08 = 183,98
2 = 5010,06 – 4826,08 = 183,98
Отсюда: σx =  35,27
35,27
σy =  13,56
13,56
I. Найдем коэффициент корреляции между Р0 и Рш
Для этого сначала рассчитаем коэффициент ковариации Сxy
Сxy= 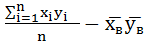 = 10219,12 – 10012,02 = 207,1
= 10219,12 – 10012,02 = 207,1
Коэффициент корреляции будет равен
rxy = Сxy/σxσy = 207,1/478,26 = 0,43
Вычислим значение произведения │rxy│  = 0,43
= 0,43  = 1,72
= 1,72  3
3
Вывод: связь недостаточно вероятна, т.е. не обоснована.
II. Составим уравнения линейной регрессии Р0 и Рш

 = 69,47+0,43*35,27/ 13,56 (х-144,17)= 69,47 + 1,12x – 161,41 =
= 69,47+0,43*35,27/ 13,56 (х-144,17)= 69,47 + 1,12x – 161,41 =
= 18,94x – 91,94

 = 144,17+0,43*13,56/ 35,27 (y-69,47)= 144,17 + 0,17y – 11,81
= 144,17+0,43*13,56/ 35,27 (y-69,47)= 144,17 + 0,17y – 11,81
 = 2,79y + 132,36
= 2,79y + 132,36
Построим точки, определенные таблицей и полученные линии регрессии.
Для построения воспользуемся вспомогательной таблицей вида:
| x | ||
 | 180,84 | 559,64 |
| Y | ||
 | 89,8 | 229,3 |
Видим, что линии регрессии на графике пересекаются достаточно близко к области скопления экспериментальных точек, но проходят не идеально точно, т.к. связь между случайными величинами х и y недостаточно вероятна (меньше 3).
Из решения системы найдем точные координаты пересечения линий регрессии:

x= - 46,58
y= 2,40
Следовательно, точка пересечения имеет координаты (- 46,58; 2,40), что мы и можем наблюдать на графике.
III. Проверим гипотезу о значимости коэффициента корреляции при уровне значимости α=0,05
Проверим нулевую гипотезу о равенстве нулю генерального коэффициента корреляции: Н0:  =0
=0
Н1:  0
0
- Вычислим наблюдаемое значение критерия по формуле:
Тнабл =  = (0,43
= (0,43  )/(
)/( )= 1,82
)= 1,82
- По таблице критических точек распределения Стьюдента найдем tдв.кр.(α;к), где α=0,05 к=n-2
tдв.кр.(0,05;17-2)=(0,05;15)= 2,13
Вывод:│Тнабл│< tдв.кр – следовательно, мы можем принять гипотезу Н0 о равенстве нулю генерального коэффициента корреляции, т.е.  не значимо отличается от нуля. Таким образом, это доказывает, что случайные величины x и y не коррелированны (нет тесной связи).
не значимо отличается от нуля. Таким образом, это доказывает, что случайные величины x и y не коррелированны (нет тесной связи).
IV. Найдем несмещенные оценки математического ожидания и
дисперсии Р0 и Рш
1. Рассчитаем несмещенные оценки математического ожидания, которые равняются выборочным средним:
 =
=  = 2451/17 =144,17
= 2451/17 =144,17
 =
=  = 1181/17 =69,47
= 1181/17 =69,47
2. Рассчитаем несмещенные оценки дисперсии (см. Задание№1):
S2несм=(n/n-1)*Dв, где Dв – исправленная оценка, которая вычисляется по формуле Dв=  2, где
2, где
 =
= 
 2=
2=  2
2
Таким образом, Dв=  –
–  2
2
Dв=374249/17 – (144,17)2 = 22014,65-20784,99=1229,66
Следовательно, S2несм(x)=17/16*1229,66=1303,44
По аналогии S2несм(y)=17/16*(85171/17-(69,47)2)=195,48
Отсюда: Sнесм(x) =  36,10
36,10
Sнесм(y) =  13,98
13,98
V. Исследуем, принадлежат ли минимальные и максимальные члены выборок к основной генеральной совокупности по правилу 3σ и критерию Стьюдента
1. Из данной выборки найдем минимальные хmin и максимальные элементы хmax
Р0max = xmax и Рш max = ymax
Р0mix = xmin Рш mix = ymin
Имеем:
xmax = 233 ymax =95
xmin = 99 ymin =52
2. По правилу 3σ определим интервалы для x и y:
Правило 3σ: нормально распределенная случайная величина с D(x)= σ2 практически не отклоняется от своего среднего значения больше чем на 3σ.
В нашем случае мы используем несмещенную оценку дисперсии D(x)= S2несм
[  - 3Sнесм;
- 3Sнесм;  + 3Sнесм]
+ 3Sнесм]
[- 46,58- 3*36,10; - 46,58+ 3*36,10]
[-154,88;61,72]
[  - 3Sнесм;
- 3Sнесм;  + 3Sнесм]
+ 3Sнесм]
[2,40- 3*13,98; 2,40+ 3*13,98]
[-39,54;44,34]
3. Проверим принадлежность элементов к найденному интервалу:
xmax  [35,04; 253,2] ymax
[35,04; 253,2] ymax  [27,53;111,41]
[27,53;111,41]
xmin  [35,04; 253,2] ymin
[35,04; 253,2] ymin  [27,53;111,41]
[27,53;111,41]
 2018-01-08
2018-01-08 2394
2394






