Предел алгебраической суммы конечного числа последовательностей равен алгебраической сумме пределов последовательностей слагаемых, если последние пределы существуют.
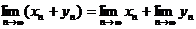
Предел произведения конечного числа последовательностей равен произведению пределов последовательностей сомножителей, если последние пределы существуют.

Предел частного последовательностей равен частному пределов числителя и знаменателя, если последние пределы существуют и предел последовательности знаменателя отличен от нуля.
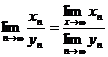
Докажем, например, первое утверждение.
Пусть имеются две последовательности {xn} и {yn} и их сумма {xn + yn}. Требуется доказать, что 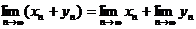
Воспользуемся определением предела последовательности.
Пусть 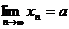 ,
, 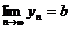 . Это значит, что для любого ε>0 существует число N, такое что│xn -a│<
. Это значит, что для любого ε>0 существует число N, такое что│xn -a│< 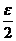 и│yn - b│<
и│yn - b│< 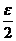 .
.
Составим модуль разности между n членом последовательности суммы и числом (а+ b) и воспользуемся для него свойствами модуля и указанными выше неравенствами.
Будем иметь
│(xn - yn) – (a + b)│= │(xn –a) + (yn – b)│<│xn- a│+│yn - b│< 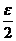 +
+ 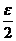 = ε
= ε
Тогда по определению предела последовательности, утверждение о пределе суммы последовательностей верно.
Аналогично доказываются остальные утверждения.
Предел функции.
Пусть функция 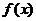 определена в некоторой окрестности точки а за исключением может быть лишь самой точки а. Рассмотрим поведение функции при стремлении аргумента х к значению а.
определена в некоторой окрестности точки а за исключением может быть лишь самой точки а. Рассмотрим поведение функции при стремлении аргумента х к значению а.
Определение 1. Число А называется пределом функции 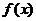 при стремлении х к а, если для любой последовательности значений аргументов
при стремлении х к а, если для любой последовательности значений аргументов 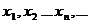 из области определения функции стремящейся к а, соответствующая последовательность значений функции
из области определения функции стремящейся к а, соответствующая последовательность значений функции 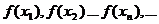 стремится к А.
стремится к А.
Обозначают это так:
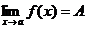
Если последовательность значений функции 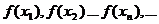 стремится к
стремится к 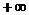 или
или 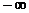 при стремлении
при стремлении 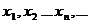 к значению а, то говорят, что предел функции равен
к значению а, то говорят, что предел функции равен 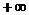 или
или 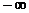 .
.
Обозначают это так:
 или
или 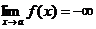
Предел функции 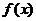 при стремлении
при стремлении 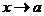 можно определить по-другому.
можно определить по-другому.
Определение 2. Число А называется пределом функции 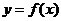 в точке а, если для
в точке а, если для 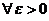 , существует
, существует 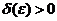 такое, что для всех х, удовлетворяющих неравенству
такое, что для всех х, удовлетворяющих неравенству 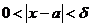 выполняется неравенство
выполняется неравенство 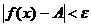 .
.
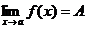
Легко доказать, что оба определения предела функции эквивалентны.
Графически определение предела можно представить так:
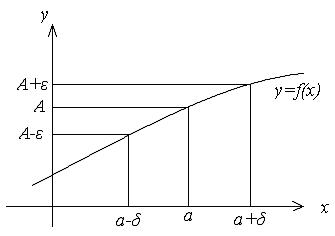
Как только значения аргумента х попадают в 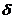 –окрестность точки а, соответствующие значения у попадают в
–окрестность точки а, соответствующие значения у попадают в 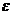 –окрестность точки А, при этом для существования предела функции при
–окрестность точки А, при этом для существования предела функции при 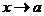 :
:
1) необязательно, чтобы функция была определена в точке а;
2) 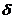 –окрестность точки а должна удовлетворять условиям симметричности, а
–окрестность точки а должна удовлетворять условиям симметричности, а 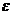 –окрестность точки А при заданной
–окрестность точки А при заданной 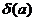 не обязательно должна удовлетворять этому требованию.
не обязательно должна удовлетворять этому требованию.
Определение 3. Число А есть предел функции 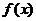 при
при 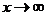 если для
если для 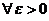 существует некоторое число М такое что неравенство
существует некоторое число М такое что неравенство 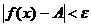 выполняется для всех х удовлетворяющих неравенству
выполняется для всех х удовлетворяющих неравенству 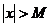
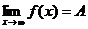
 2018-01-08
2018-01-08 425
425








