2018-01-08
1332
Рассмотрим функцию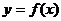 
определённую в некоторой точке 
и некоторой окрестности точки . Пусть в указанной точке функция имеет значение 
.
Определение 1. Функция 
называется непрерывной в точке , если она определена в окрестности точки, включая саму точку и 
.
Определение непрерывности можно сформулировать иначе.
Пусть функция 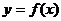определена при некотором значении , 
. Если аргументу дать приращение 
, то функция получит приращение 
.
Пусть функция в точке 
непрерывна (по первому определению непрерывности функции в точке),
тогда 
или 
.
То есть, если функция непрерывна в точке , то бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.
Справедливо и обратное предложение: если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна.
Определение 2. Функция 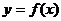называется непрерывной при 
(в точке ), если она определена в этой точке и некоторой её окрестности и если 
.
Учитывая первое и второе определение непрерывности функции в точке можно получить следующее утверждение:
|
|
|
или , но 
, тогда 
.
Следовательно, для того чтобы найти предел непрерывной функции при 
достаточно в аналитическое выражение функции вместо аргумента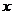 
подставить его значение .
Определение 3. Функция, непрерывная в каждой точке некоторой области называется непрерывной в этой области.
Например:
Пример 1. Доказать, что функция 
непрерывна во всех точках области определения.
Воспользуемся вторым определением непрерывности функции в точке. Для этого возьмём любое значение аргумента 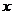и дадим ему приращение . Найдём соответствующее приращение функции
Тогда 
;
Пример 2. Доказать, что функция 
непрерывна во всех точках 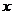из 
.
Дадим аргументу 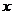приращение , тогда функция получит приращение 
Найдём 
так как функция 
, то есть ограничена.
Аналогично можно доказать, что все основные элементарные функции непрерывны во всех точках области их определения, то есть область определения элементарной функции совпадает с областью её непрерывности.
Определение 4. Если функция 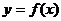непрерывна в каждой точке некоторого интервала 
, то говорят, что функция непрерывна на этом интервале.
