2018-01-08
1241
1.1. Общий вид СЛУ. В общем виде система линейных уравнений выглядит так:
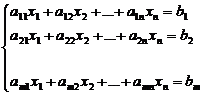
Число уравнений m может совпадать, а может и не совпадать с числом неизвестных n. Мы будем изучать лишь случай, когда m = n и для n = 3.
Рассматриваем систему 3-го порядка, т.е. систему (1) 
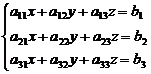
Неизвестные (переменные) – x, y, z. Решением системы с тремя переменными является упорядоченная тройка чисел (x, y, z).
Числа в правой части – свободные члены системы (b1, b2, b3).
1.2. Метод Крамера
Теорема. Если определитель системы ∆ =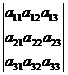 
≠ 0, то система имеет единственное решение (x, y, z), определяемое формулами Крамера: 
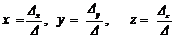, где
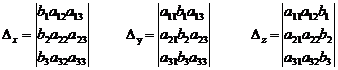
Эти определители получаются заменой соответствующего столбца на столбец свободных членов.
1.3. Практическая работа № 3 «Решение СЛУ методом Крамера»
Пример. Решить систему уравнений: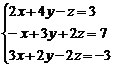 
1) Составляем и вычисляем определитель системы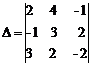 
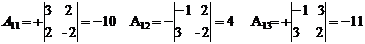
∆ = 2·(-10) + 4·4 + (-1)·(-11) = -20 + 16 + 11 = 7
2) Считаем ∆x =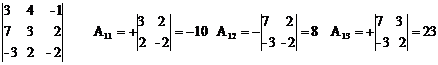 
∆x = 3·(-10) + 4·8 + (-1)·23 = -30 + 32 – 23 = -21
3) Считаем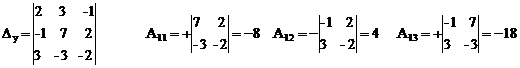 
∆y = 2·(-8) + 3·4 + (-1)·(-18) = -16 + 12 + 18 = 14
4) Считаем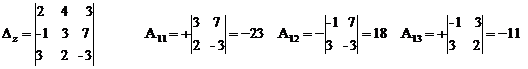 
∆z = 2·(-23) + 4·18 + 3·(-11) = -46 + 72 – 33 = -7
|
|
|
6) По формулам Крамера решение системы: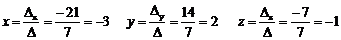 
Ответ: (-3; 2; -1)
