Лекция 2. Матричный метод и метод Гаусса

2.1. Матричный метод решения СЛУ

Рассматриваем систему уравнений (1). Для нее

Здесь: A – матрица коэффициентов, X – столбец неизвестных, B – столбец свободных членов.

Теорема. Если определитель матрицы A отличен от нуля (∆(А) ≠ 0), то система (1) имеет единственное решение, определяемое равенством X = A^{– 1}· B, где A^{– 1} – обратная матрица.

Пример: решаем ту же систему уравнений, которую решали методом Крамера

1) Составляем матрицы A и B: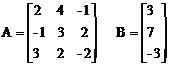

2) Ищем алгебраические дополнения для составления обратной матрицы:

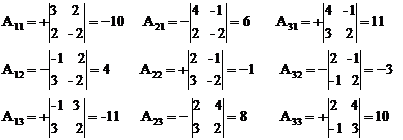
3) Определитель: ∆(А) = 7 (см. метод Крамера)

4) Тогда решение системы:

т.е. Ответ: (-3; 2; -1)

2.2. Метод Гаусса

Изложенные выше методы имеют недостатки. Главный из них – это отличие определителя системы от нуля (∆(А) ≠ 0).

Метод Гаусса основан на элементарных алгебраических преобразованиях матриц, при которых получаются эквивалентные матрицы. Эквивалентными называются матрицы, имеющие равносильную систему уравнений.

Цель: путем умножения какой-либо строки на число и сложения с другой строкой добиться нулевых коэффициентов при двух переменных. Дальше решение сводится к нахождению второй и третьей переменной путем обычной подстановки.

Расширенная матрица: Переход от одной расширенной матрице к другой будем обозначать знаком ~ или <=>.

Например, запись 2C₂+C₁ <=> … означает: строку №2 умножаем на 2 и складываем со строкой №1.

На деле приводим исходную матрицу к треугольному виду. Если при переходе матрицы A к треугольной в новой матрице не возникло ни одной нулевой строки (столбца), то исходная система имеет единственное решение.

Пример: решаем ту же систему уравнений, которую решали методами 1 и 2

Составляем расширенную матрицу системы и преобразовываем:

Тогда: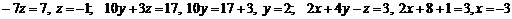

Ответ: (-3; 2; -1)