Этап 3. Определение количественной оценки ошибки выборки

Средняя ошибка выборки

Ошибка для средней:

а) Отбор бесповторный:

,

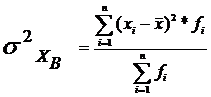где - дисперсия 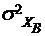показывает отклонение индивидуальных значения х_i от среднего значения индивидуального признака в выборке.

 

в) Отбор повторный

.

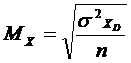Ошибка для доли альтернативного признака:

a) Отбор бесповторный.

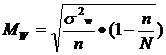
где: w - дисперсия альтернативного признака.

Дисперсия альтернативного признака рассчитывается по формуле:

.

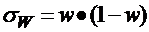в) Отбор повторный.

Этап 4. Распространение выборочных характеристик на генеральную совокупность с учетом предельной ошибки выборки

Утверждать, что обобщающие показатели ген. совокупности не выйдут за пределы средней ошибки выборки М можно только с вероятностью 0,683. Это означает, что в 683 случаях из 1000 генеральные средняя Хг и доля Р будут находиться в установленных пределах (Хв+Мх, Хв-Мх) и (w+Мw, w-Мw). В остальных 317 случаях они могут отличаться. Чтобы увеличить вероятность попадания в полученный интервал, необходимо его увеличить в t раз.

Следовательно,

 

 

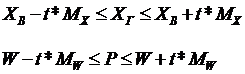
где t -коэффициент доверия

Существуют специальные таблицы, где по указанной вероятности можно найти t.

Для практических расчетов можно использовать следующую таблицу значений функции Лапласа

P	0,683	0,866	0,954	0,988	0,997	0,999
t		1,5		2,5		3,5

Содержание отчета

1. Исходные данные;

2. Расчетная часть;

3. Аналитическая записка.

4. Экономическая интерпретация полученных результатов.

Контрольный пример

 

На машиностроительном предприятии, где число рабочих составляет 5000 человек, методом случайного бесповторного отбора проведено обследование 250 рабочих. Получены следующие данные:

 

Квалификация (тарифный разряд)
Количество рабочих

Требуется определить пределы, в которых находится средний разряд рабочих предприятия, а также долю рабочих с разрядом 4 и выше, если принятая вероятность равна 0,806.

Расчетная часть

 

Обозначения:	xi	квалификация рабочего
	fi	количество рабочих i-той квалификации
	xв	средняя квалификация рабочего в выборке
	хг	средняя квалификация рабочего в генеральной совокупности
	w	доля рабочих с квалификацией 4 и выше в выборке
	xw	доля рабочих с квалификацией 4 и выше в генеральной совокупности
	t	коэффициент доверия
	Mx	ошибка выборки для средней квалификации
	Mw	ошибка выборки для доли

 

Хi	fi	Хi*fi	(Xi-Xв)2*fi
			77,284
			142,578
			30,42
			3,146
			66,978
			172,494
			492,9

Результаты.

Средний разряд в выборке	3,78 разряд
Доля рабочих в выборке с разрядом 4 и выше.	0,58
Дисперсия для средней	1,9716 разряд2
Ошибка выборки для средней	1,372 разряд
Дисперсия для доли	0,243
Ошибка выборки для доли	0,0304
Коэффициент доверия для вероятности 0,806 по таблице Стьюдента	1,3