Графический способ нахождения Моды

Заключается в построении гистограммы по имеющимся частотам, нахождение наиболее часто встречающегося интервала и вычисление Моды.

Мода и средняя величина по-разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный хотя и значительной части, но не всей совокупности. Мода по своему обобщающему значению менее точна по сравнению со средней арифметической, характеризующей совокупность в целом с учетом всех без исключения элементов совокупности.

B) Медиана

Медиана - это величина, которая делит численность упорядоченного вариационного ряда на две равные части.

Графически:

Частоты

Наблюдения

Для симметричного распределения Ме=Мо.

Существует кривая распределения. Медиана на оси абцисс - это точка, в которой ордината делит площадь на две равные части.

Одна часть имеет значения вариант меньше срединного значения (медианы), другая больше.

Для дискретного ранжированного ряда, т. е. упорядоченного по возрастанию или убыванию

а) с нечетным числом членов медианой является центральное значение.

Номер наблюдения
Возраст студентов (лет)
				Медиана

Медиана = 19 лет

Хср= (17+18+18+19+20+21+20)/7 = 19,6 лет

Номер элемента медианы = (n+1)/2.

б) При четном числе членов медианой является среднее арифметическое из двух смежных центральных вариант.

Для дискретного ранжированного ряда с вариантами Х=(1, 3, 4, 5, 7, 9)

Ме = (4+5)/2 = 4,5

В общем виде для дискретного ранжированного ряда Медиана рассчитывается по формуле:

Ме = (Х_n_/2 + X _n_/2+1)/ 2

Для интервального ряда:

1) Располагаем варианты по ранжиру.

2) Определяем для ранжированного ряда накопленные частоты.

3) По накопленным частотам находим медианный интервал. Медианным интервалом называется такой, где накопленная частота больше или равна половине всех частот å f_i /2.

4) Находим медиану по формуле

где:

Хме - нижняя граница варианты медианного интервала,

Iме - величина медианного интервала,

- полусумма накопленных частот,

S_Ме-1 - накопленные частоты перед медианным интервалом,

f_Ме - частота медианного интервала.

Пример.

Добыча угля (в тыс. тонн)	Доля шахт в процентах	Удельный ряд накопленных частот
Варианты – Хi	Частоты – fi	Si
101-300	2,6%	2,6%
301-500	8,8%	2,6+8,8=11,4%
501-1000	25,0%	11,4+25 = 36,4%
1001-2000	39,3% Модальная строка	36,4+39,3=75,7% Медианная строка
2001-выше	24,3%	75,7+24,3=100%
	Всего: 100%

Модальный интервал находится в пределах интервала 1001-2000, т. к. максимальная частота равна 39,3.

Мо =	1001	+	1000	*	(39,3-25)/(39,3-25+39,4-24,3)	=	1489,05 тыс. тонн
	Начало интервала		Величина интервала		Доля на отрезке – модальном интервале

Медианный интервал также находится в пределах интервала 1001-2000, т. к. сумма накопленных частот в этом интервале равна 75,7 и превышает полусумму накопленных частот (Sfi/2 =100/2=50)

Медиана находится внутри интервала 1001-2000 и равняется началу интервала плюс какая-то часть до середины всей совокупности (в нашем случае до 50 процентов).

Ме =	1001	+	1000	*	(50-36,4)/39,4	=	1346,2 тыс. тонн
	Начало интервала		Величина интервала		Доля на отрезке

Медиану следует применять в качестве средней, если совокупность неоднородна, велико значение крайних величин. В случае больших колебаний варьирующего признака средняя арифметическая учитывает крайние величины.

3.Дисперсия (Д или s²) и среднее квадратическое отклонение s

Среднее квадратическое отклонение равно квадратному корню из дисперсии

Эти величины служат для обоснования применения средней величины. Физический смысл дисперсии и среднего квадратического отклонения заключается в следующем. Они отражают отклонения индивидуального признака (Xi) от средней величины (Xср).

Если Мо<Me<Xср, то имеется правосторонняя ассиметрия, если Мо>Me>Xср, то имеется левосторонняя ассиметрия.

В случае ассиметрии структурные средние недостаточно адекватно отражают совокупность. Обычно в таком случае квадратическое отклонение (s) достаточно велико.

Если Мо, Ме и Хср близки друг к другу, то распределение имеет нормальный вид, Хср типична для данной совокупности и к данному статистическому распределению можно применять специальные статистические методы, например, корреляционно-регрессионный анализ.

· Дисперсия.

Дисперсия представляет собой среднее из квадратов отклонений вариантов значений признака от их средней величины. Если среднее арифметическое есть не что иное, как математическое ожидание наблюдаемого признака, то дисперсия характеризует наблюдаемые признаки с точки зрения отклонения их от среднего значения.

Дисперсия рассчитывается по несгруппированным данным по формуле:

Дисперсия по сгруппированным данным:

· Среднее квадратическое отклонение представляет собойкорень из дисперсии.

Среднее квадратическое и среднее линейное отклонения есть именованные величины.

Среднее квадратическое - это степень надежности средней величины. Чем меньше среднее квадратическое, тем лучше соответствует средняя величина.

4. В целях сопоставления уровня вариаций по разным признакам применяются относительные показатели вариации, характеризующие уровень колеблемости признака в изучаемой статистической совокупности:

Коэффициент вариации

Среднее квадратическое отклонение дает обобщенную характеристику колеблемости всех вариант совокупности. Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Для социально-экономических явлений совокупность является однородной при коэффициенте вариации до 32 ‑ 33 процентов (для распределений, близких к нормальному).

· Коэффициент осцилляции.

Коэффициент осцилляции представляет собой отношение размаха вариации к средней арифметической:

· Относительное линейное отклонение.

Относительное линейное отклонение есть отношение среднего линейного отклонения к средней арифметической:

При расчетах среднего квадратического отклонения и дисперсии промежуточные расчеты лучше выполнять в виде таблицы:

Х_i	f_i	S_i	Х_i*f_i	(X_i-X_ср)²*f_i
…	…	…	…	…
å(f_i)			å(Х_i*f_i)	å((X_i-X_ср)²*f_i)

Изучение особенностей поведения признака в исследуемой статистической совокупности непосредственно связано с изучением и учетом формы и вида распределения, к которому можно отнести случайную величину, характеризующую количественные характеристики признака. Наиболее распространенными характеристиками формы распределения являются асимметрия и эксцесс. Асимметричные ряды распределений показаны на рис. 1.

Коэффициент асимметрии отрицателен для скошенных влево распределений, равен нулю для симметричных и положителен для скошенных вправо распределений.

Распределения величин, ограниченных слева, как правило, скошены вправо (таков, например, годовой доход).

Для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель асимметрии As.

Величина показателя асимметрии A_s может быть положительной и отрицательной. Положительная величина асимметрии указывает на наличие правосторонней асимметрии. При правосторонней асимметрии между показателями центра распределения существует соотношение:

Отрицательный знак асимметрии указывает на наличие левосторонней асимметрии. При левосторонней асимметрии между показателями центра распределения существует соотношение:

Чтобы данные привести к симметричному виду, их подвергают подходящему преобразованию, например, данные с положительной асимметрией часто логарифмируют.

Распределения величин, ограниченных слева, как правило, скошены вправо (таков, например, годовой доход). Для выявления асимметрии полезно использовать гистограммы, диаграммы и графики на нормальной вероятностной бумаге.

Рис. 1 Асимметричные ряды распределений:

1) с правосторонней асимметрией,

2) с левосторонней асимметрией.

Применение этого показателя дает возможность не только определить степень асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, которая зависит от объема наблюдений и рассчитывается по формуле:

Если отношение асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если отношение асимметрия несущественна, ее наличие может быть объяснено влиянием различных случайных обстоятельств.

Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Линдбергом предложен следующий показатель для оценки эксцесса:

Ех = П- 38,29,

где П - доля (%) количества вариантов, лежащих в интервале, равном половине среднего квадратического отклонения в ту и другую сторону от средней арифметической.

Наиболее точным является показатель, основанный на использовании центрального момента четвертого порядка. Для нормального распределения характерным является следующее соотношение между центральным моментом второго и четвертого порядка:

Поэтому в качестве показателя эксцесса Ех принимается показатель:

На рисунке 2 представлены два распределения: островершинное и плосковершинное. Эксцесс качественно представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении отношение

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести изучаемое распределение к нормальному типу. Если непрерывная случайная величина имеет плотность распределения

то она подчиняется закону нормального распределения. Для построения кривой нормального распределения надо знать два параметра: среднее значение признака и среднеквадратическое отклонение s. Если средняя арифметическая не меняется (Хср = const), но растет величина среднего квадратического отклонения, распределение имеет более плосковершинный xapaктep (Рис. 3).

Рис. 3. Ряды распределения с различными СКО (σ1 < σ2 < σ1)

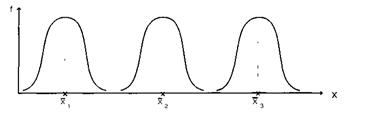
Кривые нормального распределения с одинаковыми s, но разными Хср. (Хср1<Хср2<Хср3)

На рисунке приведено «семейство» кривых нормального распределения с одной и той же величиной среднего квадратическо-го отклонения, по с разными средними (). В этом случае кривая, не меняя своей формы, сдвигается вправо вдоль оси абсцисс.