Введем новую физическую величину, характеризующую электрическое поле – поток вектора напряженности электрического поля (Φ). Понятие потока вектора 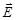 аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора
аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Фактически поток вектора 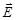 пропорционален числу линий напряженности, пронизывающих элементарную площадку Δ S (рис. 1.6).
пропорционален числу линий напряженности, пронизывающих элементарную площадку Δ S (рис. 1.6).
Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка Δ S. Произведение модуля вектора 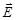 на площадь Δ S и на косинус угла α между вектором
на площадь Δ S и на косинус угла α между вектором 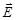 и нормалью
и нормалью 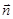 к площадке называется элементарным потоком вектора напряженности через площадку Δ S:
к площадке называется элементарным потоком вектора напряженности через площадку Δ S:
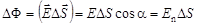 ,
,
где 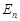 – проекция вектора
– проекция вектора 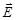 на нормаль
на нормаль 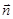 к площадке
к площадке 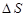 ;
; 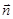 - единичный вектор, перпендикулярный площадке
- единичный вектор, перпендикулярный площадке 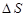 .
.
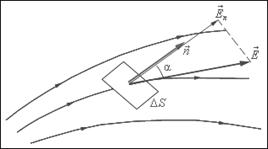
Рис. 1.6. К определению элементарного потока ΔΦ
Полный поток вектора напряженности 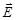 сквозь поверхность
сквозь поверхность 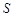 в общем случае равен:
в общем случае равен:
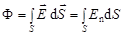 ,
,
где 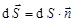 . (Выбор нормали
. (Выбор нормали 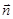 условен, но в случае замкнутых поверхностей
условен, но в случае замкнутых поверхностей 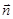 принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока - В·м.
принято брать наружу области, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль). Единица измерения потока - В·м.
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки Δ Si, определить элементарные потоки 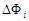 поля
поля 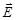 через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора
через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора 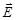 через замкнутую поверхность S (рис. 1.7):
через замкнутую поверхность S (рис. 1.7):
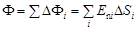 .
.
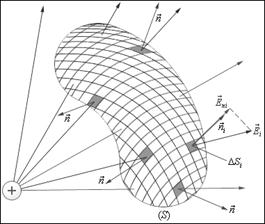
Рис. 1.7. Поток Ф через произвольную замкнутую поверхность S
Теорема Гаусса: поток вектора 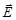 через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на
через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 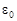 , т. е.:
, т. е.:
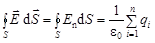 .
.
Вычисление напряженности поля системы электрических зарядов и полей, создаваемых заряженными телами различной формы, можно проводить с помощью принципа суперпозиции. Однако, во многих случаях эту задачу можно значительно упростить, используя теорему Гаусса.
Модуль напряженности электрического поля, созданного точечным зарядом 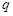 на расстоянии
на расстоянии 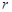 от него (рис. 1.8),
от него (рис. 1.8),
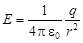 .
.
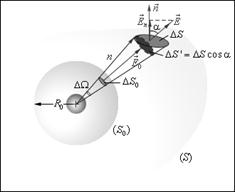
Рис. 1.8 Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд
Модуль напряженности поля диполя в точке, находящейся на расстоянии 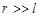 от диполя (
от диполя (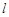 - плечо диполя),
- плечо диполя),
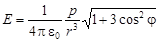 ,
,
где 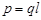 - электрический момент диполя,
- электрический момент диполя, 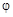 - угол между осью диполя и радиус-вектором, проведенным из центра диполя в данную точку.
- угол между осью диполя и радиус-вектором, проведенным из центра диполя в данную точку.
Вращающий момент сил, действующих на диполь во внешнем электрическом поле,
 ;
; 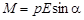 ,
,
где 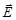 - напряженность электрического поля;
- напряженность электрического поля; 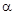 - угол между векторами
- угол между векторами 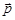 и
и 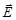 .
.
Сила, действующая на диполь во внешнем электрическом поле,
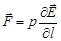 ,
,
где производная берется по направлению вектора 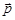 . Направление вектора
. Направление вектора 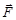 в общем случае не совпадает с направлением вектора
в общем случае не совпадает с направлением вектора 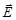 , ни с направлением вектора
, ни с направлением вектора 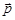 . Направление вектора силы совпадает лишь с направлением элементарного приращения вектора
. Направление вектора силы совпадает лишь с направлением элементарного приращения вектора 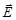 , взятого в направлении
, взятого в направлении 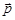 .
.
Выражения для модулей напряженности электрических полей симметричных объектов имеют вид:
1. Напряженность поля равномерно заряженной сферической поверхности в точках, лежащих вне и внутри сферы на расстоянии 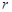 от ее центра
от ее центра
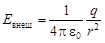 ;
; 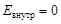 .
.
2. Напряженность поля бесконечно длинной равномерно заряженной нити или бесконечно длинной равномерно заряженной цилиндрической поверхности в точках, расположенных вне ее,
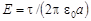 ,
,
где 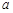 - расстояние точки от нити (оси цилиндра),
- расстояние точки от нити (оси цилиндра), 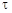 - линейная плотность заряда, численно равная заряду, приходящемуся на единицу длины нити или цилиндра:
- линейная плотность заряда, численно равная заряду, приходящемуся на единицу длины нити или цилиндра:
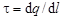 .
.
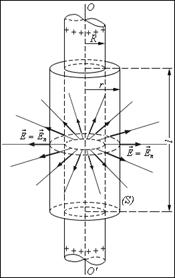
Рис. 1.9. Вычисление поля однородно заряженного цилиндра.
OO ' – ось симметрии цилиндра
3. Напряженность поля бесконечной равномерно заряженной плоскости (рис. 1.10)
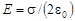 ,
,
где 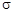 - поверхностная плотность заряда, численно равная заряду, приходящемуся на единицу площади заряженной поверхности:
- поверхностная плотность заряда, численно равная заряду, приходящемуся на единицу площади заряженной поверхности:
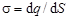 .
.
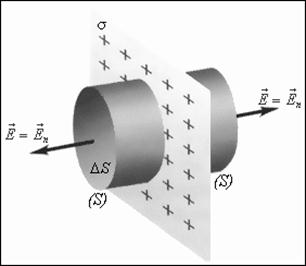
Рис. 1.10 Поле равномерно заряженной плоскости
4. Напряженность поля двух бесконечных, параллельных плоскостей, равномерно заряженных с поверхностной плотностью заряда 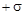 и
и 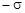 (поле плоского конденсатора) в точках, расположенных между плоскостями и вне их, соответственно равны
(поле плоского конденсатора) в точках, расположенных между плоскостями и вне их, соответственно равны
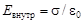 ,
, 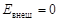 .
.
Потенциал. Разность потенциалов
Потенциальная энергия взаимодействия двух точечных зарядов, находящихся на расстоянии 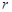
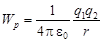 .
.
Потенциал электрического поля является энергетической скалярной характеристикой электрического поля и равен отношению потенциальной энергии положительного пробного точечного заряда, помещенного в данную точку поля, к величине этого заряда:
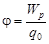 ,
,
где 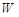 – потенциальная энергия заряда
– потенциальная энергия заряда 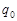 , помещенного в данную точку электрического поля. Потенциальная энергия бесконечно удаленной точки принимается равной нулю. Единица потенциала – вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж.
, помещенного в данную точку электрического поля. Потенциальная энергия бесконечно удаленной точки принимается равной нулю. Единица потенциала – вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж.
Работа, совершенная силами поля по перемещению положительного заряда 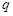 из точки 1 в точку 2:
из точки 1 в точку 2:
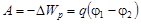 или
или 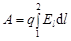 ,
,
где 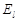 - проекция вектора напряженности
- проекция вектора напряженности 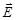 на направление
на направление 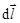 ; при этом интегрирование производится вдоль любой линии, соединяющей точки 1 и 2 (рис. 1.11).
; при этом интегрирование производится вдоль любой линии, соединяющей точки 1 и 2 (рис. 1.11).
Интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.
Теперь предположим, что заряд q 0 перемещается из произвольной точки за пределы поля (на бесконечность), где потенциальная энергия, а значит и потенциал, равны нулю, то работа сил электростатического поля 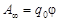 , откуда получим:
, откуда получим:
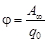 .
.
Данное выражение позволяет сформулировать еще одно определение потенциала. Потенциал – это физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки пространства в бесконечность (потенциал бесконечно удаленной точки равен нулю).
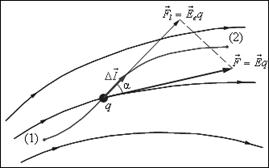
Рис. 1.11. Работа сил поля при малом перемещении заряда q
Разность потенциалов и модуль напряженности электрического поля
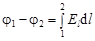 ;
; 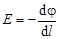 ,
,
где производная 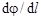 берется в направлении быстрейшего изменения потенциала, т. е. вдоль силовой линии (рис. 1.12).
берется в направлении быстрейшего изменения потенциала, т. е. вдоль силовой линии (рис. 1.12).
Для однородного поля (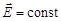 )
)
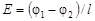 ,
,
где 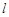 - расстояние между двумя точками, измеренное вдоль силовой линии.
- расстояние между двумя точками, измеренное вдоль силовой линии.
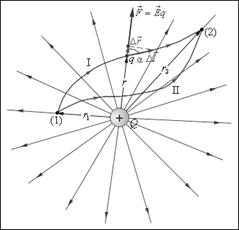
Рис. 1.12. Работа кулоновских сил при перемещении заряда q зависит только от расстояний r 1 и r 2
Потенциал поля точечного заряда 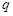 на расстоянии
на расстоянии 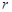 от него
от него
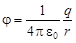 .
.
Потенциал поля сферической поверхности (шара) радиуса 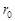 , по которой равномерно распределен заряд
, по которой равномерно распределен заряд 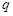 :
:
1. 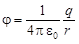 - для точек, лежащих вне сферы (шара) на расстоянии
- для точек, лежащих вне сферы (шара) на расстоянии 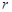 от ее центра;
от ее центра;
2. 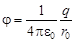 - для точек, лежащих на поверхности сферы (шара) или внутри нее.
- для точек, лежащих на поверхности сферы (шара) или внутри нее.
Потенциал электрического поля внутри непроводящего шара, равномерно заряженного по объему,
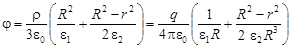 ,
,
где 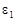 – диэлектрическая проницаемость материала шара;
– диэлектрическая проницаемость материала шара; 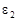 – диэлектрическая проницаемость среды, в которой находится шар.
– диэлектрическая проницаемость среды, в которой находится шар.
Принцип суперпозиции для потенциала электрического поля. Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности:
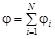 ,
,
где 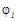 – потенциал электрического поля, созданного
– потенциал электрического поля, созданного 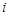 -м зарядом.
-м зарядом.
Для графического изображения потенциала используются эквипотенциальные поверхности – это поверхности во всех точках которых потенциал имеет одно и то же значение. Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. В любой точке эквипотенциальной поверхности силовая линия ей перпендикулярна, следовательно, перпендикулярен и вектор 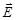 (рис. 1.13).
(рис. 1.13).
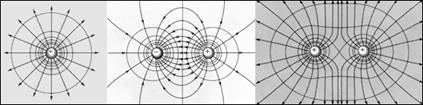
Рис. 1.13. Эквипотенциальные поверхности и силовые линии простых электрических полей: точечный заряд; электрический диполь; два равных положительных заряда
Диэлектрики в электрическом поле
Диэлектриками называются вещества, которые в обычных условиях практически не проводят электрический ток. Различают три типа диэлектриков:
1) Неполярные диэлектрики. Это диэлектрики с неполярными молекулами, симметричные молекулы которых в отсутствие внешнего поля имеют нулевой дипольный момент (например, N2, H2, O2, CO2).
2) Полярные диэлектрики. Это диэлектрики с полярными молекулами, молекулы которых вследствие асимметрии имеют ненулевой дипольный момент (например, H2O, NH3, SO2, CO).
3) Ионные диэлектрики (например NaCl, KCl). Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков.
Если диэлектрик помещен во внешнее электрическое поле, то в его объеме возникает собственное макроскопическое поле, которое всегда противоположно ориентировано по отношению к внешнему полю. Такое явление называется поляризацией диэлектрика, и оно объясняется тем, что в его объеме возникает суммарный дипольный электрический момент молекул. Различают три основных вида поляризации:
1) Электронная или деформационная поляризациядиэлектрика с неполярными молекулами - за счет деформации электронных орбит возникает индуцированный дипольный момент у атомов или молекул диэлектрика (рис. 1.14).
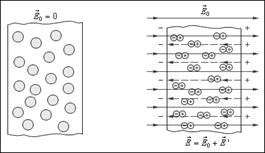
Рис. 1.14. Деформационная поляризация неполярного диэлектрика
2) Ориентационная или дипольная поляризациядиэлектрика с полярными молекулами - ориентация имеющихся дипольных моментов молекул по полю (эта ориентация тем сильнее, чем больше напряженность электрического поля и чем ниже температура) (рис. 1.15).
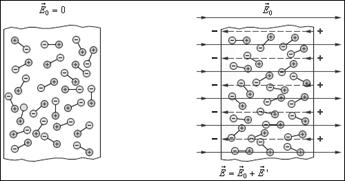
Рис. 1.15. Поляризация полярного диэлектрика
3) Ионная поляризация диэлектрика с ионными кристаллическими решетками - смещение подрешетки положительных ионов вдоль поля, а отрицательных ионов против поля приводит к возникновению дипольных моментов.
Количественной мерой поляризации диэлектрика служит вектор 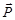 , называемый поляризованностью вещества (вектор поляризации)
, называемый поляризованностью вещества (вектор поляризации)
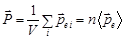 ,
,
где 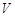 – физически малый объем вещества;
– физически малый объем вещества; 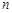 – концентрация молекул;
– концентрация молекул; 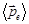 – средний дипольный момент одной молекулы. Таким образом вектор поляризации
– средний дипольный момент одной молекулы. Таким образом вектор поляризации 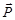 измеряется суммарным электрическим моментом всех молекулярных диполей в единице объема диэлектрика.
измеряется суммарным электрическим моментом всех молекулярных диполей в единице объема диэлектрика.
Для изотропного диэлектрика вектор 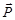 пропорционален напряженности
пропорционален напряженности 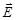 поля внутри него
поля внутри него
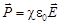 ,
,
где 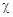 - диэлектрическая восприимчивость диэлектрика.
- диэлектрическая восприимчивость диэлектрика.
Вследствие поляризации на поверхности диэлектрика появляются нескомпенсированные заряды, которые называются связанными 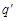 (в отличие от свободных зарядов, которые создают внешнее поле).
(в отличие от свободных зарядов, которые создают внешнее поле).
Поверхностная плотность 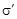 связанных зарядов равна проекции вектора
связанных зарядов равна проекции вектора 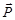 на внешнюю нормаль к поверхности диэлектрика:
на внешнюю нормаль к поверхности диэлектрика:
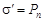 .
.
Напряженность поля внутри диэлектрика равна:
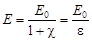 ,
,
где 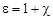 - диэлектрическая проницаемость среды, характеризующая способность диэлектриков поляризоваться в электрическом поле и показывающая во сколько раз поле ослабляется диэлектриком. Таким образом, диэлектрическая проницаемость среды
- диэлектрическая проницаемость среды, характеризующая способность диэлектриков поляризоваться в электрическом поле и показывающая во сколько раз поле ослабляется диэлектриком. Таким образом, диэлектрическая проницаемость среды
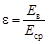 ,
,
где 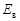 – напряженность поля в вакууме;
– напряженность поля в вакууме; 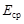 – напряженность поля в среде. Диэлектрическая проницаемость является безразмерной величиной и характеризует способность диэлектриков поляризоваться в электрическом поле, а также показывает во сколько раз поле ослабляется диэлектриком
– напряженность поля в среде. Диэлектрическая проницаемость является безразмерной величиной и характеризует способность диэлектриков поляризоваться в электрическом поле, а также показывает во сколько раз поле ослабляется диэлектриком
Для характеристики поля в диэлектрике вводится вектор электрического смещения (электрической индукции), который для изотропного диэлектрика записывается так
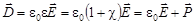 .
.
Единица электрического смещения – Кл/м2. Вектор 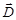 описывает электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
описывает электростатическое поле, создаваемое свободными зарядами (т. е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Введение в рассмотрение векторов поляризации и электрического смещения позволяет изменить запись и формулировку теоремы Гаусса.
Теорема Гаусса: поток вектора  через замкнутую поверхность равен алгебраической сумме свободных зарядов qi, охватываемых этой поверхностью
через замкнутую поверхность равен алгебраической сумме свободных зарядов qi, охватываемых этой поверхностью
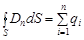 .
.
 2014-02-24
2014-02-24 37652
37652
