Разложение вектора ускорения на касательную и нормальную составляющие.
Введем обозначения:  –единичный вектор касательной к кривой,
–единичный вектор касательной к кривой,  – единичный вектор главной нормали к кривой,
– единичный вектор главной нормали к кривой,  – вектор скорости. Дифференцируя последнее, получим:
– вектор скорости. Дифференцируя последнее, получим:

учитывая, что  получим:
получим:

отсюда следует, что вектор ускорения  лежит в плоскости векторов
лежит в плоскости векторов  и
и  , т.е. в соприкасающейся плоскости. Вектор а не имеет составляющей по бинормали к траектории,
, т.е. в соприкасающейся плоскости. Вектор а не имеет составляющей по бинормали к траектории,  – касательное или тангенциальное ускорение;
– касательное или тангенциальное ускорение;  – нормальное ускорение. Тангенциальное ускорение меняет скорость только по модулю, нормальное ускорение меняет ее только по направлению. Общее ускорение определяется формулой:
– нормальное ускорение. Тангенциальное ускорение меняет скорость только по модулю, нормальное ускорение меняет ее только по направлению. Общее ускорение определяется формулой: 
Движение по окружности, вектор угловой скорости и углового ускорения.
Вращательное движение- движение точки по концентрической окружности вокруг ее центра. Понятие угловой скорости и углового ускорения относится к движению точки по окружности.
Угловая скорость- это производная от угла поворота по времени. Вектор угловой скорости:

Угловое ускорение- скорость изменения угловой скорости.
|
|
|
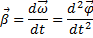
 2018-01-08
2018-01-08 2982
2982
