Экзамен по матану.
Модуль 1: Элементарные функции и пределы.
Числовая последовательность. Предел последовательности; сходящейся и расходящейся последовательности. Теорема о единственности предела сходящейся последовательности (с доказательством).
Последовательностью называется любой счётный набор действительных чисел а 1, а 2, а 3,…, аn,….
Примеры:
| 1). 1, 1, 1,…,1,…; аn =1, n Î N; | 3). 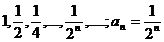 ; n Î N; ; n Î N; |
2). 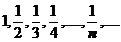 ; аn = ; аn = 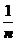 , n Î N; , n Î N; | 4). 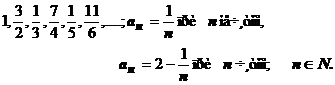 |
Число а называется пределом последовательности 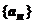 , если для любого положительного числа e существует такое натуральное число N (зависящее от e), что для членов последовательности с номерами n > N выполняется неравенство | an - a |<e.
, если для любого положительного числа e существует такое натуральное число N (зависящее от e), что для членов последовательности с номерами n > N выполняется неравенство | an - a |<e.
Обозначения: 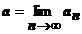 ;
; 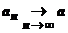 ;
; 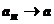 при
при 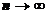 .
.
Если 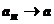 при
при 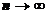 , то говорят также, что последовательность
, то говорят также, что последовательность 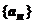 сходится к числу а.
сходится к числу а.
Краткая форма записи определения: 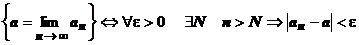 .
.
Неравенство | an - a |<e эквивалентно двустороннему неравенству -e< an - a <e или a -e< an < a +e. Таким образом, смысл неравенства | an - a |<e заключается в том, что для "e>0 мы можем найти такое N, что все точки an с номерами индексов n > N лежат внутри интервала U e(a) = (a -e, a +e), т.е. вне этого интервала лежит не более чем конечное число точек последовательности.
Теор. Последовательность может иметь не более одного предела.
Док-во. От противного: предположим, что последовательность имеет два предела: 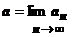 и
и 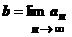 . Предположим для определённости, что b > a. Возьмём в качестве e любое число, меньшее, чем (b - a)/2. Так как
. Предположим для определённости, что b > a. Возьмём в качестве e любое число, меньшее, чем (b - a)/2. Так как 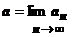 , то, по определению предела последовательности, $ N 1: n > N 1 Þ a -e< an < a +e< a +(b - a)/2=(a + b)/2. Так как
, то, по определению предела последовательности, $ N 1: n > N 1 Þ a -e< an < a +e< a +(b - a)/2=(a + b)/2. Так как 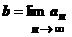 , то $ N 2: n > N 2 Þ(a + b)/2= b -(b - a)/2< b -e< an < b +e. Возьмём N =max{ N 1, N 2}. Тогда при n > N одновременно должны выполняться неравенства an < (a + b)/2 и an > (a + b)/2, что невозможно.
, то $ N 2: n > N 2 Þ(a + b)/2= b -(b - a)/2< b -e< an < b +e. Возьмём N =max{ N 1, N 2}. Тогда при n > N одновременно должны выполняться неравенства an < (a + b)/2 и an > (a + b)/2, что невозможно.
Ограниченная числовая последовательность. Теорема об ограниченности сходящейся числовой последовательности. Признак Вейерштрасса сходимости монотонной последовательности (формулировка).
Если последовательность сходится, то она ограничена.
Док-во. Пусть $ 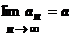 . Возьмём e=1. $ N: n > N Þ a -1< an < a +1. Итак, все члены последовательности, начиная с N +1, ограничены снизу числом a -1, сверху - числом a +1. Вне окрестности U 1(a) точки a может лежать не более N членов. Возьмём в качестве нижней границы число М 1=min{ a1, a2, a3,…, aN, a -1}, в качестве верхней границы число М 2=max{ a1, a2, a3,…, aN, a +1}. Тогда М 1
. Возьмём e=1. $ N: n > N Þ a -1< an < a +1. Итак, все члены последовательности, начиная с N +1, ограничены снизу числом a -1, сверху - числом a +1. Вне окрестности U 1(a) точки a может лежать не более N членов. Возьмём в качестве нижней границы число М 1=min{ a1, a2, a3,…, aN, a -1}, в качестве верхней границы число М 2=max{ a1, a2, a3,…, aN, a +1}. Тогда М 1 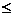 an
an 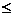 М 2, т.е. последовательность
М 2, т.е. последовательность 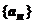 действительно ограничена.
действительно ограничена.
Признак Вейерштрасса (или теорема Вейерштрасса) звучит так: если числовая последовательность является ограниченной сверху (снизу) и является неубывающей (невозрастающей), то она имеет бесконечный предел.
Определение по Коши конечного и бесконечного предела функции в точке и на бесконечности. Односторонние пределы функции. Определение предела функции по Гейне. Теорема о связи двустороннего предела функции в точке с односторонними пределами (с доказательством).
(Коши) Пусть а - предельная точка области определения Х функции f (x). Число b называется пределом функции при х, стремящемся к а, если для любого числа e>0 существует такое число d (вообще говоря, положительное и зависящее от e), что если х Î Х принадлежит также проколотой d-окрестности 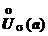 точки а, то значение функции f (x) принадлежит e-окрестности числа b.
точки а, то значение функции f (x) принадлежит e-окрестности числа b.
Обозначения:  ; f (x)® b при x ® а;
; f (x)® b при x ® а; 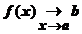 .
.
Краткая форма записи: 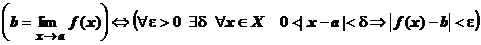 .
.
Односторонние пределы функции.
Опр. Число b называется пределом функции f (x) при х ® а справа (или правым, правосторонним пределом), если для любого числа e>0 существует такое число d, что если х Î Х удовлетворяет неравенству a < x < а +d, то | f (x)- b |<e.
Обозначения: 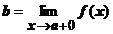 ; f (x)® b при x ® а +0;
; f (x)® b при x ® а +0; 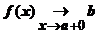 ; f (а +0).
; f (а +0).
Опр. Число b называется пределом функции f (x) при х ® а слева (или левым, левосторонним пределом), если для любого числа e>0 существует такое число d, что если х Î Х удовлетворяет неравенству a -d < x < а, то | f (x)- b |<e.
Обозначения: 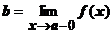 ; f (x)® b при x ® а -0;
; f (x)® b при x ® а -0; 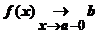 ; f (а -0).
; f (а -0).
Односторонние пределы на бесконечности:
Опр. Число b называется пределом функции f (x) при х ®+µ, если для любого числа e>0 существует такое число K, что если х Î Х удовлетворяет неравенству x > K, то | f (x)- b |<e.
Обозначения: 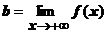 ; f (+µ).
; f (+µ).
Опр. Число b называется пределом функции f (x) при х ®-µ, если для любого числа e>0 существует такое число K, что если х Î Х удовлетворяет неравенству x < K, то | f (x)- b |<e.
Обозначения: 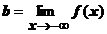 ; f (-µ).
; f (-µ).
(Гейне) Пусть { xn | xn Î X, xn ¹ a } - последовательность точек области определения функции f (x), сходящаяся к точке а. Если для любой такой последовательности { xn } последовательность значений функции { f (xn)} сходится к числу b, то b называется пределом f (x) при x ® а.
 2018-01-08
2018-01-08 4572
4572