Ограниченные и локально ограниченные функции. Теорема о локальной ограниченности функций, имеющей конечный предел (с доказательством)

Теорема (о локальной ограниченности функции, имеющей предел). Для функции f(x), имеющей (конечный) предел при x → x₀ существует проколотая окрестность этой точки, на которой данная функция ограничена.

Доказательство. Пусть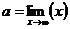

Тогда для положительного числа 1 найдетсяδ> 0 такое, что при 0 < |x — x0| <δ выполняется неравенство |f (x) — a| < 1. Отсюда

|f(x)| = |f(x) — a + a| ≤|f(x) — a| + |a| < 1 + |a|, т.е. |f(x)| < 1 + |a|,

и мы видим, что f (x) ограничена в проколотой δ-окрестности (x₀ — δ, x₀) U (x₀, x₀ + δ) точки x₀. Теорема доказана.

Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой (с доказательством).

Опр. Функция f (x) называется бесконечно малой при х ® a, если .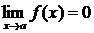

БМ обладают всеми свойствами функций, имеющих предел.

Теор. (о связи функции с её пределом). Для того, чтобы функция f (x) имела предел, равный b, при х ® a, необходимо и достаточно, чтобы f (x) представлялась в виде f (x)= b +a(х), где a(х) - БМ при при х ® a.

Док-во. Необходимость. Пусть $ 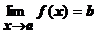. Обозначим a(х)= f (x) - b, докажем, что a(х) - БМ при при х ® a. По определению предела "e>0 $d: 0<| x - a |<dÞ| f (x) - b |=|a(х)|<e, т.е. a(х) удовлетворяет определению БМ.

Достаточность. Для доказательства достаточно прочитать доказательство необходимости в противоположном порядке.

Теорема о сумме конечного числа бесконечно малых функций (с доказательством). Теорема о произведении бесконечно малой на ограниченную (с доказательством).