Основные формулы по физике Ч. 1

Кинематическое уравнение движения материальной точки

вдоль оси x:

x = f (t),

где f(t) - некоторая функция времени.

Средняя скорость:

 

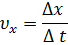
Средняя путевая скорость:

 

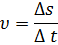
где Δ s - путь, пройденный точкой за интервал Δ t.

Мгновенная скорость:

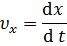
Среднее ускорение:

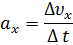
Мгновенное ускорение:

 

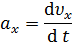
Кинематическое уравнение движение материальной точки по окружности:

φ = f(t); r = R = const.

Угловая скорость:

 

 

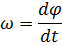
Угловое ускорение:

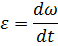
Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:

v = ω R; a _τ = ε R; a_n= ω ²R,

где v - линейная скорость; a _τ и a_n -тангенциальное и нормальное ускорения; ω - угловая скорость; ε - угловое ускорение; R - радиус окружности.

Полное ускорение:

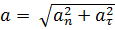или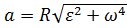

Угол между полным ускорением а и нормальным an:

α = arccos(a_n/a).

Кинематическое уравнение гармонических колебаний материальной точки:

x = Acos( ω t+ φ ),

где x - смещение, А - амплитуда колебаний, ω - круговая или циклическая частота, φ - начальная фаза.

Скорость материальной точки, совершающей гармонические колебания:

v = -A ω Sin( ω t+ φ ).

Ускорение материальной точки, совершающей гармонические колебания:

a = -A w² Cos( ω t+ φ ).

Период колебаний математического маятника:

;

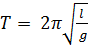где l - длина маятника, g - ускорение свободного падения.

Период колебаний физического маятника:

;

 

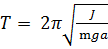где J - момент инерции относительно оси вращения, m – масса тела, а - расстояние от оси вращения до центра масс тела.

Импульс тела:

p = mv,

где m - масса тела, v - скорость тела.

Второй закон Ньютона:

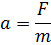
где F - cила, действующая на тело, m - масса тела.

Силы, рассматриваемые в механике:

а) сила упругости F = -kx,

где k - коэффициент упругости, x - абсолютная деформация;

б) сила тяжести F = mg,

в) сила трения F = fN,

где f - коэффициент трения, N - сила нормального давления.

Закон сохранения импульса:

Кинетическая энергия тела, движущегося поступательно:

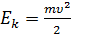или

Потенциальная энергия:

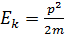
а) упругодеформированной пружины:

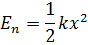
б) тела, находящегося в однородном поле силы тяжести:

E_n = mgh,

где h - высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R - радиус Земли).

Закон сохранения механической энергии:

E = E_k+E_n = const.

Основное уравнение вращательного движения относительно неподвижной оси:

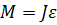
где M - результирующий момент внешних сил, действующих на тело, ε - угловое ускорение, J - момент инерции тела относительно оси вращения.

Моменты инерции некоторых тел массы m относительно оси, проходящей через центр масс:

а) стержня длины l относительно оси, перпендикулярной к стержню:

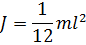
б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной к плоскости обруча (совпадающей с осью цилиндра):

J = mR²,

где R - радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной к плоскости диска:

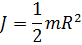
Момент инерции тела относительно произвольной оси (теорема Штейнера):

J = J₀ + ma² ,

где J₀ - момент инерции тела относительно оси, проходящей через центр масс параллельно заданной оси; m - масса тела; а – расстояние между осями.

Момент импульса тела, вращающегося относительно неподвижной оси:

L = J ω,

где ω - угловая скорость тела.

Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси:

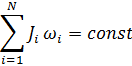
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:

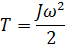
Количество вещества однородного газа (в молях):

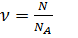или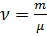

где N - число молекул газа; N_A - число Авогадро; m - масса газа; μ -молярная масса газа.

Уравнение Клапейрона - Менделеева (уравнение состояния идеального газа):

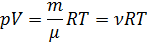
где p - давление газа, V - обьем газа, m - масса газа; μ – молярная масса газа, R - универсальная газовая постоянная, ν = m /μ - количество вещества, T - термодинамическая температура Кельвина.

Опытные газовые законы, являющиеся частными случаями уравнения Клапейрона - Мендлеева для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс T =const, m =const):

pV = const,

б) закон Гей-Люссака (изобарический процесс: p= const, m =const):

V / T = const,

в) закон Шарля (изохорический процесс: V= const, m =const):

p / T = const.

Закон Дальтона, определяющий давление смеси газов:

p = p₁+p₂+... +p_n,

где p_i - парциальные давления компонент смеси, n – число компонентов смеси.

Концентрация молекул (число молекул в единице объёма):

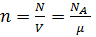ρ

где N - число молекул, содержащихся в данной системе, ρ - плотность вещества.

Основное уравнение кинетической теории газов:

,

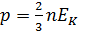где < w_п> - средняя кинетическая энергия поступательного движения молекулы.

Средняя кинетическая энергия поступательного движения молекулы:

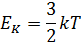
где k - постоянная Больцмана.

Средняя полная кинетическая энергия молекулы:

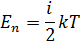
где i - число степеней свободы молекулы.

Зависимость давления газа от концентрации молекул и температуры:

p = nkT.

Скорости молекул:

а) средняя квадратичная ,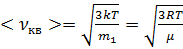

б) средняя арифметическая ,

в) наиболее вероятная ,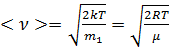

где m₁ - масса одной молекулы.

Удельные теплоёмкости газа при постоянном объёме (C_v) и при постоянном давлении (C_р):

.

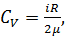
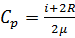Связь между удельной (с) и молярной (С) теплоёмкостями:

c = C/ μ.

Уравнение Роберта Майера:

C_p - C_v = R.

Внутренняя энергия идеального газа:

Первое начало термодинамики:

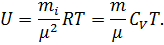
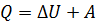
где Q - теплота, сообщенная системе (газу); Δ U – изменение внутренней энергии системы; А- работа совершенная системой против внешних сил.

Работа расширения газа:

а) в общем случае: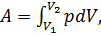

б) при изобарическом процессе: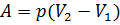

в) при изотермическом процессе: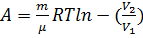

с) при адиабатическом процессе: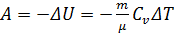

или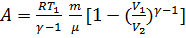

где γ = C _p/ C _v - показатель адиабаты.

Уравнения Пуассона, связывающие параметры идеального газа при адиабатическом процессе:

, , .

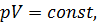
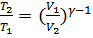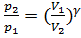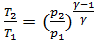Термический к.п.д. цикла:

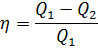
где Q₁ - теплота, полученная телом от нагревателя; Q₂ - теплота, переданная рабочим телом охладителю.

Термический к.п.д. цикла Карно:

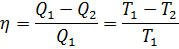
где Т₁ и Т₂ - термодинамические температуры нагревателя и охладителя.