Характеристики точності

 

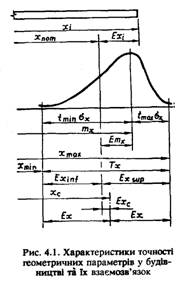
Точність геометричного пара-метра х, яким позначають випадкову величину, визначають характерис-тиками точності (рис. 4.1).

При цьому точність кутових величин може бути охарактеризована точністю лінійних розмірів, за якими визначаються ці величини.

Точність геометричного пара-метра х у кожному окремому випадку характеризується значенням дійсного відхилення Ехі.

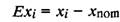(4.1.),

де Хі, Хnот — відповідно дійсне і номінальне значення параметра х.

Дійсне відхилення Ехі є кількісним виразом систематичних і випадкових похибок, накопичених при виконанні технологічних операцій і вимірювань.

Точність геометричних параметрів у стандартах та інших нормативних документах, а також на робочих креслен­нях характеризується мінімальним Хтіп і максимальним Хтax граничними розмірами, нижнім Е_Хinf і верхнім Е_Хsир граничними відхиленнями від номінального значення Хnот, допуском Тх і відхиленням Ех_с середини поля допуску Тс або середини поля допуску Хс від номінального значення Хnоm параметра Ех.

Половина допуску Тх/2 є граничним відхиленням параметра х від середини поля допуску Хс.

Взаємозв'язок між цими характеристиками точності визначається за формулами

 

 

Значення нижнього і верхнього граничних відхилень Е_Хinf і Е_Хsuр підставляють у формули зі своїми знаками.

Точність геометричного параметра х в сукупності його дійсних значень хі, здобутих у результаті виконання певного технологічного про­цесу або операції масового і серійного виробництва, визначається ста­тистичними характерами точності.

За статистичну характеристику точності геометричного параметра беруть його середнє значення т_х і середнє квадратичне відхилення Ех. У разі потреби при різних законах розподілу параметра х використовуються й інші статистичні характеристики точності.

При нормальному розподілі геометричного параметра х оцінкою ха­рактеристик тх і Ех є вибіркове середнє значення хт і вибіркове середнє квадратичне відхилення Sх, які обчислюються за формулами

	;

,

 

де п — об'єм вибірки.

 

Систематичне відхилення Етх геометричного параметра х обчислю­ється за формулою

.

Оцінкою систематичного відхилення Етх за нормальним розподілом геометричного параметра є вибіркове середнє відхилення Ехт, тобто середнє значення відхилень у вибірці, визначене за формулою

	.

 

Граничні значення Хтіп і Хтax установлюють як значення геометрич­ного параметра х, що відповідають визначеним імовірностям появи значень цього геометричного параметра х нижче Хтіп і вище Хтax. Взає­мозв'язок граничних значень Хтіп і Хтax і статистичних характеристик точності тх і Ех виражається формулами

		;

,

де t_тіп і t_тax — значення стандартизованої випадкової величини, що залежить від імовірності появи значень нижче Хтіп і вище Хтax і типу статистичного розподілу параметра х.

Як правило, ймовірність появи значень Хтіп і Хтax беруть однаковою, але не більшою за 0,05.

Кращі значення величини t за нормальним законом розподілу параметра х залежно від допустимої ймовірності появи значень х нижче Хтіп і вище Хтax, що характеризується заданим рівнем дефектності за ГОСТ 23616—79, установлені ГОСТ 23615—79. У разі симетрич­ного (наприклад, нормаль-ного) розподілу геометричного параметра х (рис. 4.2) і однакової ймовірності появи значень Хі нижче Хтіп і вище Хтax (t тіп = t max = t) взаємозв'язок між характеристиками точності, на­веденими у формулах (4.2) і (4.7), має такий вигляд:

	;

.

;

 

Якщо при цьому середнє значення тх параметра практично не відрізняється від його номінального значення Хnот, то взаємозв'язок характеристик точності виражається формулами

 

 

		;

;

.

;