2018-01-21
485
Передаточна функція розімкненого кола ( :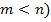
| 
|
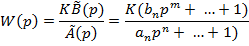
Цей випадок відповідає системам автоматичного керування без астатизму.
Введемо допоміжну функцію:
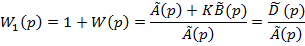
де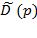 
- характеристичний багаточлен замкненої системи,
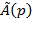-характеристичний багаточлен розімкненого кола цієї системи.
Підставимо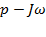 
і одержимо: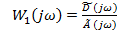 
За критерієм Михайлова зміна аргументу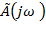 
при зміні 
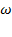від 0 до +∞ повинна дорівнювати 
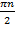, тому що передбачається, що розімкнене коло стійке.
З іншого боку, потрібно, щоб система була стійкою в замкненому стані. Для цього потрібно поставити вимогу, щоб зміна аргументу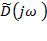 
при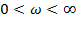 
також дорівнювала 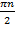. Звідси випливає, що зміна аргументу повинна бути:
- 
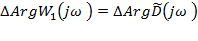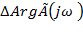=0.
Це значить, що годограф не повинен охоплювати початок координат.
Повернемося тепер до функції: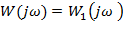 
-1, що являє собою амплітудно-фазову частотну характеристику розімкненого кола.
Годограф: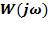 
не повинен охоплювати точку (- 1; 0j) на дійсній вісі.
Частотний критерій Найквіста:
якщо розімкнене коло системи стійке, то для стійкості замкненої системи необхідно і достатньо, щоб амплітудно-фазова частотна характеристика розімкненого кола не охоплювала точку (-1, j0).
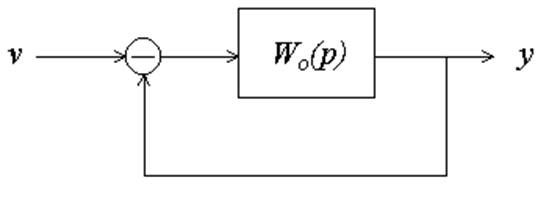
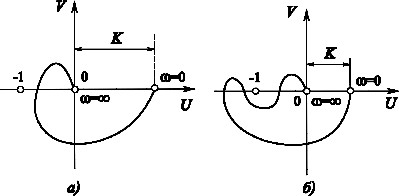
Годограф на рис.10.4а відповідає випадку, коли стійкість системи порушиться тільки зі збільшенням загального коефіцієнта підсилення розімкненого кола К, а на рис.10.4б — випадку, коли і при зменшенні К система може стати нестійкою.
| 
|
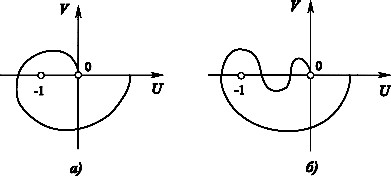
Рис.10.4 Рис.10.5
При складних обрисах амплітудно-фазових характеристик (клювоподібного вигляду як на рис. 10.5б і більш складних), до записаного вище формулювання частотного критерію додається роз'яснення, що розуміти під терміном «неохоплення точки (-1; j0)». Характеристика може перетинати від’ємну вісь лівіше точки (-1; j0), але тоді число позитивних (зверху вниз) переходів характеристики через вісь абсцис лівіше точки (- 1; j0) повинно дорівнювати числу негативних переходів (знизу нагору).
