Диференціальні рівняння руху ідеальної рідини

Розглянемо рух елементарного об’єму рідини у вигляді паралелепіпеда, подумки виділеного нами з потоку ідеальної рідини.

Рівняння руху ідеальної рідини можна одержати з диференціальних рівнянь рівноваги (спокою) такого ж самого елементарного об’єму рідини, якщо, згідно принципу Д’аламбера, до діючих сил (масових і поверхневих) приєднати сили інерції (див. рис. 3 і рівняння (22). Тоді сума проекцій всіх сил, включаючи сили інерції на відповідні осі повинна дорівнювати нулю.

Сили інерції в проекціях на відповідні осі, віднесені до одиниці маси (як і всі сили, прикладені до елементарного об’єму, що знаходяться в стані спокою) ввійдуть в рівняння руху відповідно до осей зі знаком мінус: ; ; .

Тоді система диференціальних рівнянь для рухомої частинки рідини за час dt в проекціях на відповідні осі буде мати наступний вигляд:

(71)

Ця система рівнянь встановлює зв’язок між проекціями масових сил, швидкостями, тиском і густиною рідини і називається системою диференціальних рівнянь Л. Ейлера. Вони є основою для вивчення самих головних питань гідродинаміки.

Якщо розглядати рух реальної рідини, тоді додатково до розглянутих сил додаються сили тертя. В результаті отримаємо систему диференціальних рівнянь Нав’є-Стокса.

Рівняння Бернуллі для елементарної струминки ідеальної рідини. Для виведення цього рівняння застосовуємо систему диференціальних рівнянь Ейлера (71).Оскільки проекції прискорень ; ; ― повні диференціали і є функціями координат і часу (x, y, z, t), то їх необхідно записати через часткові похідні. Тоді система рівнянь записується так:

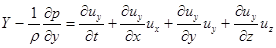(72)

(так як, наприклад, для осі ” x ”

,

і в свою чергу: ; ; ).

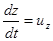Аналогічно буде і для інших осей (як написано вище).

Для усталеного руху 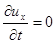; ; 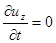, тоді система рівнянь (72), запишеться так:

 

(73)

Помножимо перше рівняння даної системи на dx, причому рівняння ліворуч множимо на dx, а праворуч на ; друге ― на dy і третє ― на dz.

Система диференціальних рівнянь буде:

.

Так як ; ; 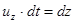, то вирази в дужках будуть повними диференціалами du_x; du_y; du_z. Тоді

(74)

Далі складемо дані рівняння за вертикаллю (в стовпчик), причому u_x, u_y, u_z введемо під диференціал

.

В дужках маємо повний диференціал тиску dp, а ліворуч 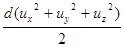, що дорівнює . Тоді

(75)

Розглянемо випадок, коли з масових сил на рідину в елементарній струминці діє тільки сила ваги, яка має прискорення ” g ” земного тяжіння. Тобто: х = 0; y = 0; z = - g.

Тоді рівняння (75) запишеться .

Поділимо це рівняння на (- g) і дістанемо:

. (76)

Рівняння (76) називається рівнянням Бернуллі в диференціальній формі. Воно застосовується як для газів (при ≠ const) так і для рідин, для яких = const.

Для краплинної рідини (і газів з ρ = соnst) інтеграл рівняння (76) буде

. (77)

Для двох перерізів вздовж елементарної струминки ідеальної рідини рівняння Бернуллі буде мати наступний вигляд

, (78)

де всі величини мають розмірність довжини (метри стовпа рідини), м.ст.р.

Рівняння Бернуллі розглядається відносно площини порівняння, яка проводиться нижче перерізів, або через нижній переріз.

z₁, z₂ – з геометричної точки зору представляють відстань центрів ваги відповідних поперечних перерізів до площини порівняння, а з енергетичної – питомі потенціальні енергії положення;

і – з геометричної точки зору представляють п’єзометричні напори (напори стовпчиків рідини в п’єзометричних трубках, які створюють відповідні тиски р₁ і р₂ на осі елементарної трубки, або труби). З енергетичної – питомі потенціальні енергії тиску;

і – з геометричної точки зору представляють швидкісні напори, а з енергетичної – питомі кінетичні енергії, якими володіє рідина, що проходить через перший і другий перерізи.

Сума трьох напорів в будь яких перерізах вздовж елементарної струминки ідеальної рідини відносно площини порівняння називається повним гідродинамічним напором (позначається Н_d) і є сталою величиною, тобто Н_d1 = Н_d2.

Проілюструємо це на рис. 28.

В потоці рідини подумки виділимо елементарну струминку, яка розташована на осі труби. В кожному поперечному перерізі (на ділянках з плавнозмінним рухом) встановимо по дві тонкі скляні трубки. Перша – п’єзометрична, друга – гідродинамічна. Гідродинамічна трубка (як видно на рис. 28) проходить в середину елементарної струминки, кінець якої загнутий на 90^о і розташований на осі струминки, отвором назустріч потоку.

Якщо в перерізі 1-1 тиск р₁, то в п’єзометричній трубці рідина підніметься на висоту . Одночасно в гідродинамічній трубці (загнутий кінець якої співпадає з віссю п’єзометра) рідина підніметься на висоту (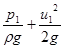), так як на кінець гідродинамічної трубки діє не тільки тиск р₁ а і кінетична енергія частинок рідини, яка перетворюється в потенціальну енергію тиску.

В другому перерізі на величину п’єзометричного напору буде впливати перехід частини геометричного напору z₁ в п’єзометричний (у нашому випадку він збільшується на величину z₁ - z₂ і в той же самий час зменшується на величину у зв’язку зі збільшенням швидкісного напору у другому перерізі за рахунок перетворення частини п’єзометричного напору у швидкісний (за законом нерозривності руху рідини ).

Як видно з рівняння (78) і рис. (28), повний гідродинамічний напір в першому перерізі Н_d1 дорівнює повному гідродинамічному напору в другому перерізі Н_d2, тобто Н_d1 = Н_d2.

Рівняння Бернуллі для елементарної струминки реальної рідини приймає наступний вигляд

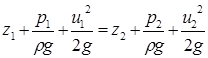+ (79)

де – втрати напору при русі реальної рідини в елементарній струминці від першого до другого перерізів.

Втрати напору виникають за рахунок наявності сил тертя на поверхнях суміжних елементарних струминок, які рухаються з різними швидкостями.

Як видно з рівняння Бернуллі (79) і рис 29, повний гідродинамічний напір в другому перерізі Н_d2 менший за Н_d1 на величину втрат напору між цими перерізами, тобто Н_d1 - Н_d2. = .

Швидкісний напір в другому перерізі той же самий що і при русі ідеальної рідини, так як на впливають тільки dQ і dF₂, а вони – сталі величини.

 

Властивість живих перерізів на ділянках з плавнозмінним рухом потоку рідини.

Перша властивість. На ділянках з плавно змінним рухом рідини живий переріз буде плоский оскільки лінії течії паралельні між собою і нормальні в кожній точці до площини живого перерізу і називаються площею поперечного перерізу. Площа поперечного перерізу (в циліндричній трубі) нормальна до твірної циліндричної поверхні.

Друга властивість. У площі поперечного перерізу гідродинамічний тиск за вертикаллю підпорядковується основному рівнянню гідростатики (рис 30), тобто

Доведемо другу властивість. Якщо координатна вісь х направлена вздовж осі потоку (циліндричної труби), то проекція складових векторів швидкості u_у і u_z в будь-яких точках на ділянках з плавнозмінним рухом на осі у і z будуть дорівнювати нулю, а вектор складової u_х буде співпадати з напрямом координати х. Тобто

u_х = u; u_у = 0; u_z = 0.

Тоді система диференціальних рівнянь для рухомої частини рідини на ділянках з плавнозмінним рухом на площині у о z (в площі поперечного перерізу) буде

 

 

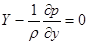(80)

Два останніх рівняння показують, що гідродинамічний тиск в живому перерізі на ділянках з плавно змінним рухом підпорядковуються основному рівнянню гідростатики.