Коническое сечение имеет фокус и директрису. У эллипса и гиперболы есть ещё один фокус и директриса. Действительно, пусть коническое сечение – эллипс:
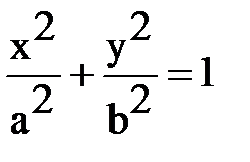 . (1)
. (1)
В каноническом расположении его директриса 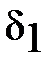 параллельна оси у, а фокус
параллельна оси у, а фокус 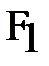 расположен на оси х. Такой эллипс симметричен, в частности, относительно оси у, поэтому у него есть фокус
расположен на оси х. Такой эллипс симметричен, в частности, относительно оси у, поэтому у него есть фокус 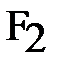 и директриса
и директриса 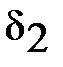 , симметричные фокусу
, симметричные фокусу 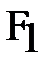 и директрисе
и директрисе 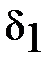 .
.
Аналогичным рассуждением устанавливается существование 2-х фокусов и двух директрис у гиперболы
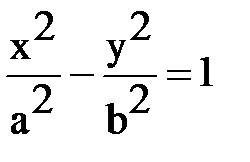 . (2)
. (2)
Теорема. Сумма расстояний от произвольной точки эллипса до его фокусов постоянна, т.е. не зависит от точки.
Теорема. Разность расстояний от произвольной точки гиперболы до ее фокусов постоянна.
Пусть c – расстояние от центра эллипса (1) до фокусов. Сумма расстояний от вершины (o, b) до фокусов равна 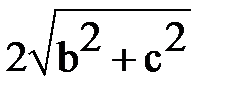 . Сумма расстояний от вершины (а, о) до фокусов равна 2а. Эти суммы должны быть равны
. Сумма расстояний от вершины (а, о) до фокусов равна 2а. Эти суммы должны быть равны 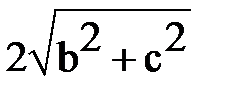 =2а,
=2а, 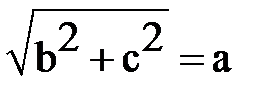 ,
, 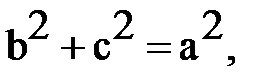
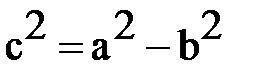 . (3).
. (3).
Следовательно, для эллипса 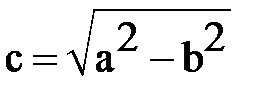 . (3 ´)
. (3 ´)
Пусть с – расстояние от центра гиперболы (2) до фокусов.
Для гиперболы справедливо другое соотношение 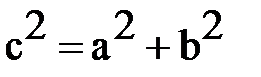 , (4)
, (4)
откуда
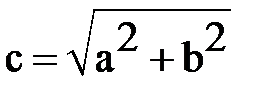 . (4´)
. (4´)
 2017-11-01
2017-11-01 1534
1534








