| A |
| B |
предельное положение секущей AB, когда точка B неограниченно
приближается к точке A. Если кривая задана уравнением y=f(x), то
касательная к ней в точке A (x0,y0) определяется известным уравнением
y - y0 = f’(x0)(x - x0) (1)
Аналогично, если кривая является графиком функции x =  , то уравнение касательной будет
, то уравнение касательной будет
 , (2)
, (2)
где производная берется по y.
Составим уравнения касательных к коническим сечениям. Каноническое уравнение параболы y2 = 2px запишем в виде  . Производная:
. Производная:  .
.
Тогда уравнение касательной в точке (x0,y0) в форме (2) будет иметь вид

Учитывая, что точка (x0,y0) лежит на параболе, т.е.  , окончательно получим
, окончательно получим

Замечание. Уравнение касательной к параболе легко запомнить, если преобразовать уравнение параболы следующим образом:  и вместо одной пары (x,y) подставить (x0,y0).
и вместо одной пары (x,y) подставить (x0,y0).
Пусть (x0,y0) – точка эллипса  Выразим y:
Выразим y:

Верхней полуплоскости соответствует знак «+», а нижней «-». Найдем производную функции, задающей верхнюю часть эллипса,
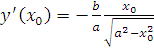 .
.
 2017-11-01
2017-11-01 1422
1422
