Оптическое свойство эллипса

 

Теорема. Световые лучи, исходящие из одного фокуса эллипса, после зеркального отражения от эллипса проходят через второй фокус.

Иными словами, с касательной к эллипсу в любой точке М отрезк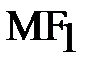и и 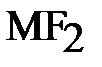образуют равные углы .

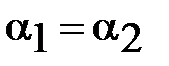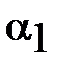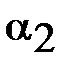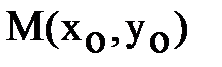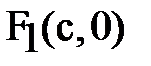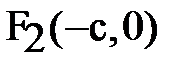Уравнение касательной к эллипсу (1) в точке 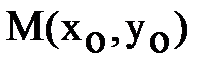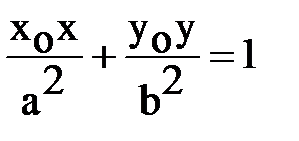. Её угловой коэффициент: К = .

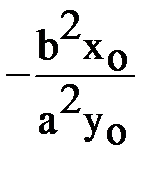Уравнение прямой, проходящей через точки :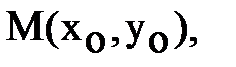

, , ,

.

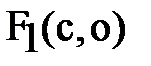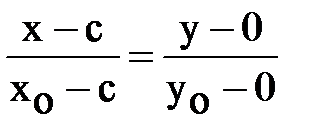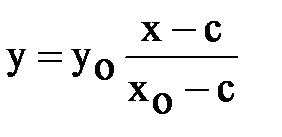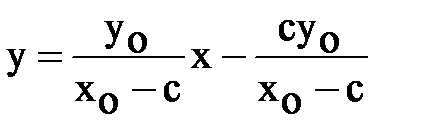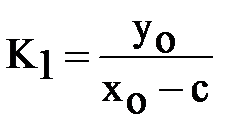Заменяя с на -с, получим угловой коэффициент 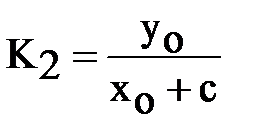прямой .

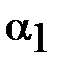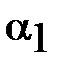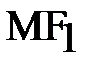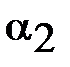Найдём tg угла от касательной до фокального радиуса и tg угла 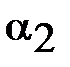от фокального радиуса до касательной:

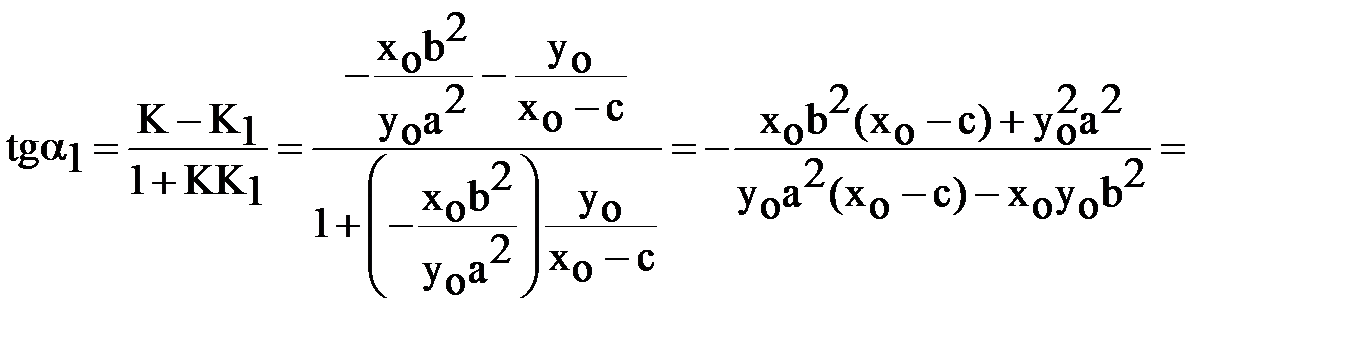
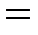
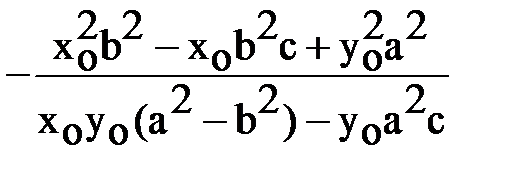. (5).

Точка 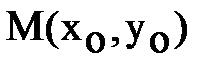лежит на эллипсе (1), т.е. , .

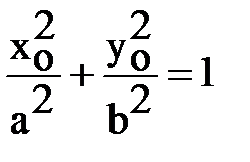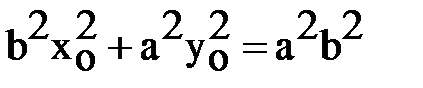Подставим это тождество и формулу (3) в равенство (5):

.

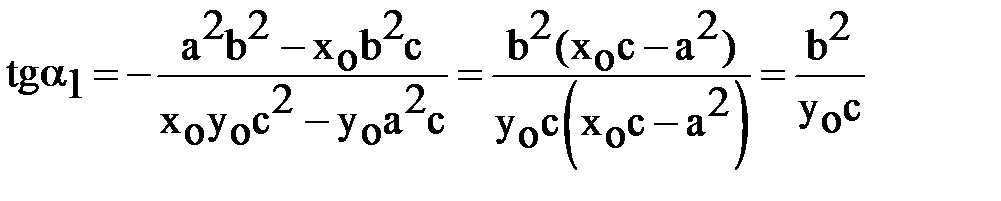Аналогично

.

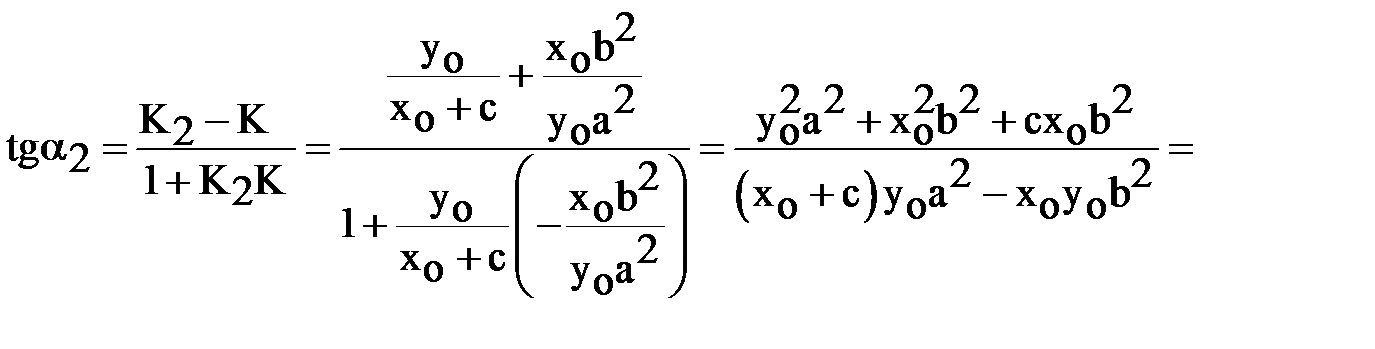
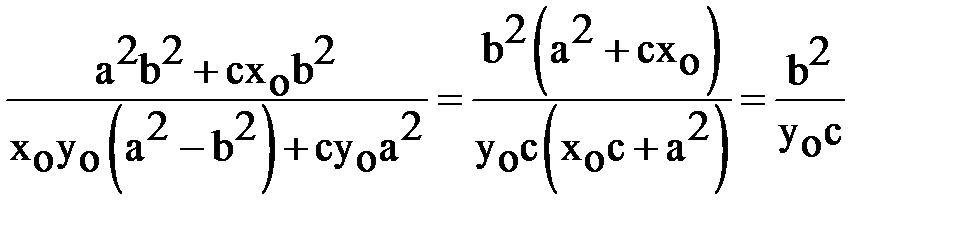Аналогичным свойством обладает гипербола. Световые лучи, исходящие из одного фокуса, после зеркального отражения от гиперболы, кажутся исходящими из другого фокуса.

Оптическое свойство параболы состоит в том, что лучи света, исходящие из фокуса, после отражения от параболы образуют параллельный пучок:

 

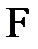Упражнение 22. Найтидиректрисы конических сечений в каноническом расположении.

Упражнение 23. Показать, что все конические сечения 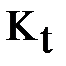, задаваемые уравнениями 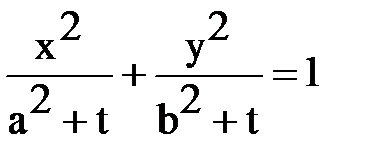, где 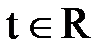- параметр семейства сечений, софокусны, т.е. имеют общие фокусы. Доказать, что через каждую точку 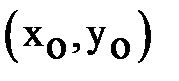плоскости х у, (не принадлежащую осям координат) проходит два конических сечения семейства - эллипс и гипербола, пересекающиеся в этой точке под прямым углом, т.е. касательные к ним в точке 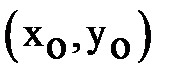перпендикулярны.