Тема 1. Векторная алгебра.
Лекция 1.
Линейная алгебра.
МФЮА. МАСИ. Соболева В.В.
Системы координат на плоскости. Векторы и линейные операции над ними. Проекция вектора на ось. Разложение вектора на компоненты. Скалярное произведение векторов, его свойства, физический и геометрический смысл. Векторы в пространстве. Векторное произведение векторов, его свойства, физический и геометрический смысл. Смешанное произведение трех векторов, его свойства и геометрический смысл..
Системы координат на плоскости
Декартовы прямоугольные координаты (рис. 4.1)
О - начало координат, Ох - ось абсцисс, Оy - ось ординат, 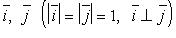 - базисные векторы,
- базисные векторы, 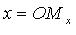 - абсцисса точки M (
- абсцисса точки M (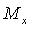 - проекция точки M на ось Ох параллельно оси Оy),
- проекция точки M на ось Ох параллельно оси Оy), 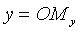 - ордината точки M (
- ордината точки M (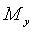 - проекция точки M на ось Oy параллельно оси Ox).
- проекция точки M на ось Oy параллельно оси Ox).
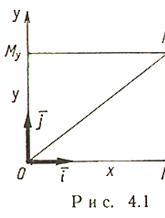
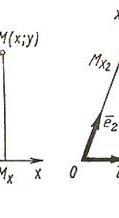
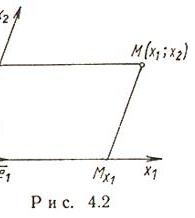
Декартовы косоугольные (афинные) координаты (рис. 4.2)
О - начало координат, 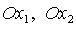 - оси координат,
- оси координат, 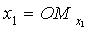 ,
, 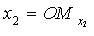 - координаты точки M (
- координаты точки M (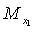 - проекция точки M на ось
- проекция точки M на ось 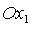 параллельно оси
параллельно оси 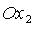 , аналогично
, аналогично 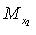 ),
), 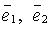 - базисные векторы.
- базисные векторы.
Полярные координаты (рис. 4.3)
О - полюс, Ox - полярная ось, 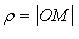 - полярный радиус,
- полярный радиус, 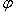 - полярный угол.
- полярный угол.
Главные значения 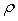 и
и 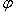 :
: 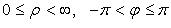 (иногда
(иногда 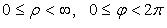 ).
).
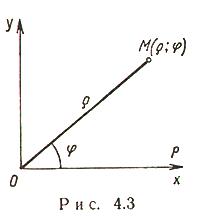
Выражение декартовых прямоугольных координат через полярные
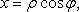
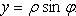
Выражение полярных координат через декартовы прямоугольные
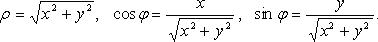
 2014-02-02
2014-02-02 4641
4641