 |
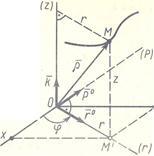
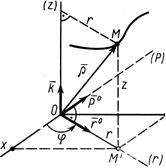
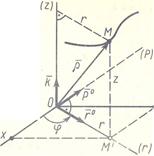
При движении точки в пространстве иногда используются цилиндрические оси координат. Они получаются добавлением к полярным координатам на плоскости координаты z, отчисляемой вдоль неподвижной оси Oz (рис. 11). Положение точки М определяют заданием трёх её цилиндрических координат как функций времени:
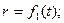
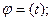
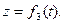
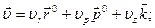
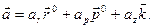
 |
 |
где 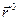 ,
, 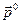 ,
, 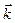 - единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.
- единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.
Представим радиус – вектор 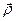 точки М как сумму двух векторов, т.е.
точки М как сумму двух векторов, т.е.

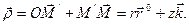
Скорость точки получим дифференцированием радиуса – вектора 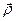 по времени:
по времени:
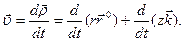
Первое слагаемое в этом выражении вычислялось при выводе формулы для скорости точки в полярных координатах. Было получено
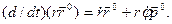
Во втором слагаемом постоянным по модулю и направлению единичный вектор 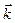 можно вынести за знак производной. Для скорости получается следующее разложение на составляющие, параллельные осям цилиндрической системы координат:
можно вынести за знак производной. Для скорости получается следующее разложение на составляющие, параллельные осям цилиндрической системы координат:
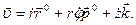
Отсюда получаем формулы для проекций скорости на цилиндрические оси координат:
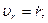
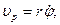
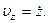
Так как составляющие скорости 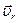 ,
, 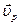 и
и 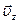 , параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем
, параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем
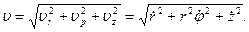
Ускорение точки получим дифференцированием по времени вектора скорости:
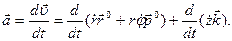
Первое слагаемое в этом выражении вычислялось при выводе ускорения в полярных координатах:
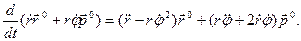
Во втором слагаемом при дифференцировании выносим вектор 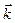 за знак производной. Объединяя результаты дифференцирования, получим следующее разложение ускорения на составляющие, параллельные осям цилиндрической системы координат:
за знак производной. Объединяя результаты дифференцирования, получим следующее разложение ускорения на составляющие, параллельные осям цилиндрической системы координат:
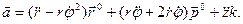
Отсюда получаем формулы для проекций ускорения на цилиндрические оси координат
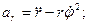
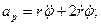
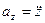 .
.
Составляющие ускорения 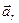 ,
, 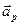 и
и 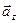 , взаимно перпендикулярны, поэтому для модуля ускорения имеем:
, взаимно перпендикулярны, поэтому для модуля ускорения имеем:
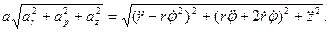
 2014-02-17
2014-02-17 6842
6842
