Определители матриц, их свойства и нахождение

Каждой квадратной матрице можно поставить в соответствие некоторое число, вычисляемое по определенному правилу и называемое определителем.

Необходимость введения понятия определителя – числа, характеризующего квадратную матрицу порядка n, тесно связано с решением систем линейных алгебраических уравнений.

Определитель матрицы А будем обозначать: | А | или D.

Определителем матрицы первого порядка А = (а ₁₁) называется элемент а ₁₁. Например, для А = (-4) имеем | А | = -4.

Определителем матрицы второго порядка называется число, определяемое по формуле

| А | = .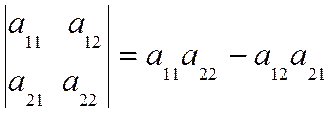

Например, | А | = .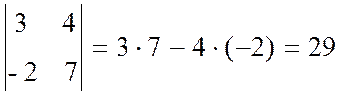

Определителем матрицы третьего порядка называется число, определяемое по формуле

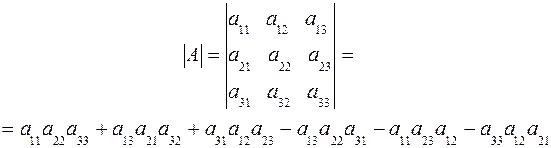
Это число представляет алгебраическую сумму шести произведений, при этом у первых трех произведений знак не меняется, а у последних – меняется на противоположный. Формулу (1.4) можно легко запомнить, используя следующую схему, называемую правилом треугольника или правилом Саррюса:

+ -

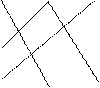Словами это правило можно записать так: со своим знаком надо взять произведение элементов, соединенных главной диагональю, и произведения элементов, соединенных вершинами треугольников, у которых основание параллельно главной диагонали. С обратным знаком берутся аналогичные произведения, только относительно побочной диагонали.

Например,

| А | =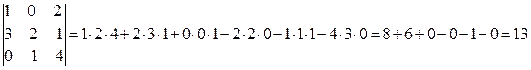

Определение определителя матрицы n -го порядка давать не будем, а лишь покажем метод его нахождения.

В дальнейшем, вместо слов определитель матрицы n -го порядка будем говорить просто определитель n -го порядка. Введем новые понятия.

Пусть дана квадратная матрица n -го порядка.

Минором М _ij элемента а _ij матрицы А называется определитель (n -1)-го порядка, полученный из матрицы А вычеркиванием i -ой строки и j -го столбца.

Алгебраическим дополнением А_ij элемента а_ij матрицы А называется его минор, взятый со знаком (-1)^i+j:

А _ij = (-1)^i+j М _ij,

т.е. алгебраическое дополнение либо совпадает со своим минором, когда сумма номеров строки и столбца – четное число, либо отличается от него знаком, когда сумма номеров строки и столбца – нечетное число.

Например, для элементов а ₁₁ и а ₁₂ матрицы А = 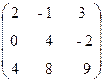миноры

М ₁₁ = А ₁₁ = ,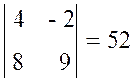

М ₁₂ = ,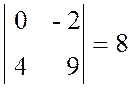

а А ₁₂ = (-1)¹⁺² М ₁₂ = -8.

Теорема (о разложении определителя). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения, т.е.

| А | = а _i1 A _i1 + а _i2 A _i2 + … + а _in A _in,
для любого i = 1, 2, …, n

или

| А | = а _1j A _1j + а _2j A _2j + … + а _nj A _nj,

для любого j = 1, 2, …, n

Первая формула называется разложением определителя по элементам i -ой строки, а вторая – разложением определителя по элементам j -го столбца.

Нетрудно понять, что с помощью этих формул любой определитель n -го порядка можно свести к сумме определителей, порядок которых будет на 1 меньше и т.д. пока не дойдем до определителей 3-го или 2-го порядков, вычисление которых уже не представляет трудности.

Для нахождения определителя могут быть применены следующие основные свойства:

1. Если какая-нибудь строка (или столбец) определителя состоит из нулей, то и сам определитель равен нулю.

2. При перестановке любых двух строк (или двух столбцов) определитель умножается на -1.

3. Определитель с двумя одинаковыми или пропорциональными строками (или столбцами) равен нулю.

4. Общий множитель элементов любой строки (или столбца) можно вынести за знак определителя.

5. Величина определителя не изменится, если все строки и столбцы поменять местами.

6. Величина определителя не изменится, если к одной из строк (или к одному из столбцов) прибавить другую строку (столбец), умноженную на любое число.

7. Сумма произведений элементов какой-нибудь строки (или столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю.

8. Определитель произведения двух квадратных матриц равен произведению их определителей.

Введение понятия определителя матрицы позволяет определить еще одно действие с матрицами – нахождение обратной матрицы.

Для каждого ненулевого числа существует обратное число, такое, что произведение этих чисел дает единицу. Для квадратных матриц тоже существует такое понятие.

Матрица А ^-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица, т.е.

А × А ^-1 = А ^-1× А = Е.

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица будет квадратной того же порядка. Однако не каждая квадратная матрица имеет свою обратную.

Матрица А называется невырожденной или неособенной, если ее определитель 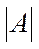отличен от нуля. В противном случае, матрица называется вырожденной или особенной.

Теорема (о существовании обратной матрицы). Любая неособенная матрица имеет обратную.

Матрицу 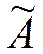, элементы которой являются алгебраическими дополнениями соответствующих элементов матрицы А, назовем дополнительной к данной матрице А.

Обратная матрица определяется по формуле

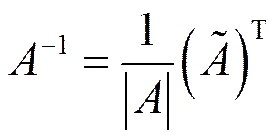
Обратная матрица обладает следующими свойствами:

1.

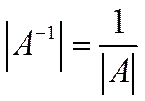
2.

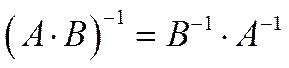
3.

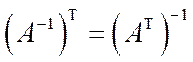
Из формулы вытекает следующее правило нахождения обратной матрицы.

Для того чтобы для матрицы А найти обратную нужно:

1) найти определитель 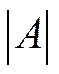матрицы;

2) найти дополнительную матрицу ;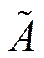

3) транспонировать дополнительную матрицу, т.е. найти ;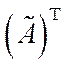

4) разделить каждый элемент транспонированной дополнительной матрицы на значение определителя 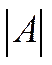исходной матрицы.