10.1. – 10.10. Исследовать на сходимость числовые ряды.
10.1. а)  ; ;
| б)  ; ;
| |
10.2. а)  ; ;
| б)  ; ;
| |
10.3. а)  ; ;
| б)  ; ;
| |
10.4. а)  ; ;
| б)  ; ;
| |
10.5. а)  ; ;
| б)  ; ;
| |
10.6. а) 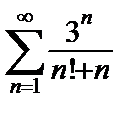 ; ;
| б)  ; ;
| |
10.7. а)  ; ;
| б)  ; ;
| |
10.8. а)  ; ;
| б)  ; ;
| |
10.9. а)  ; ;
| б)  ; ;
| |
10.10. а)  ; ;
| б)  . .
| |
10.11. – 10.20. Найти интервал сходимости степенного ряда.
10.11.  ; ;
| 10.12. 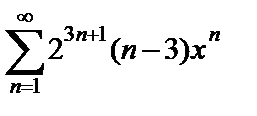 ; ;
|
10.13.  ; ;
| 10.14.  ; ;
|
10.15.  ; ;
| 10.16.  ; ;
|
10.17.  ; ;
| 10.18.  ; ;
|
10.19.  ; ;
| 10.20. 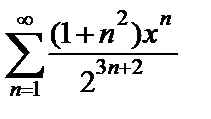 . .
|
10.21. – 10.31. Вычислить определенный интеграл с точностью до 0,01, разложив подынтегральную функцию в степенной ряд и затем проинтегрировав его почленно.
10.21. 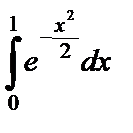 ; ;
| 10.22. 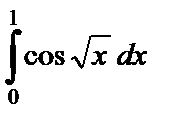 ; ;
|
10.23. 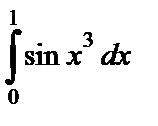 ; ;
| 10.24. 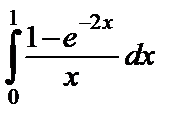 ; ;
|
10.25.  ; ;
| 10.26.  ; ;
|
10.27.  ; ;
| 10.28.  ; ;
|
10.29.  ; ;
| 10.30. 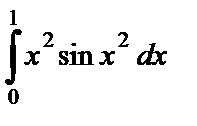 . .
|
XI. Ряды Фурье. Математическая физика. Функция
комплексной переменной. Операционное исчисление.
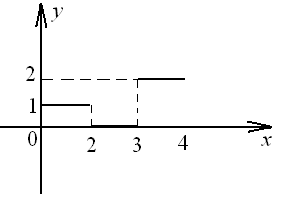
11.1. –11.10. Разложить в тригонометрический ряд Фурье функцию, заданную графически.
11.1.

| 11.2.
|
11.3.

| 11.4.

|
11.5.

| 11.6.

|
11.7.

| 11.8.

|
11.9.
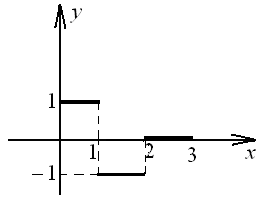
| 11.10.

|
11.11. – 11.20. Методом Даламбера найти закон 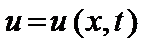 колебаний бесконечной струны, описываемой уравнением
колебаний бесконечной струны, описываемой уравнением  и начальными условиями:
и начальными условиями: 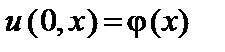 ,
,  , если
, если
11.11.  , ,
| 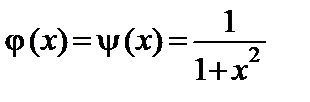 . .
| |
11.12.  , ,
|  , ,
|  . .
|
11.13.  , ,
|
 , ,
|  . .
|
11.14.  , ,
|  , ,
|
 . .
|
11.15.  , ,
|
 , ,
| 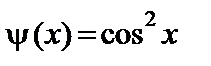
|
11.16.  , ,
|  , ,
|  . .
|
11.17.  , ,
|  , ,
|  . .
|
11.18.  , ,
| 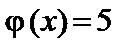 , ,
|  . .
|
11.19. 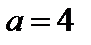 , ,
| 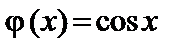 , ,
| 
|
11.20.  , ,
|
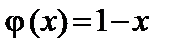 , ,
|
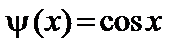 . .
|
11.21. – 11.30. Дана действительная 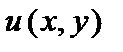 (мнимая
(мнимая  ) часть аналитической функции
) часть аналитической функции  комплексной переменной
комплексной переменной  . Требуется: а) найти
. Требуется: а) найти 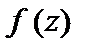 ; б)
; б)  в точке
в точке 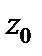 .
.
11.21.  , ,
|
 . .
|
11.22.  , ,
|  . .
|
11.23.  , ,
|
 . .
|
11.24.  , ,
|  . .
|
11.25. 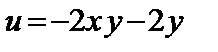 , ,
|  . .
|
11.26. 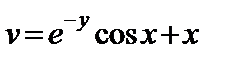 , ,
|  . .
|
11.27.  , ,
|
 . .
|
11.28. 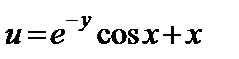 , ,
|  . .
|
11.29.  , ,
|  . .
|
11.30.  , ,
|  . .
|
11.31. – 11.40. Методом операционного исчисления найти частное решение дифференциального уравнения.
11.31. 
|   . .
|
11.32. 
|   . .
|
11.33. 
|   . .
|
11.34. 
|
  . .
|
11.35. 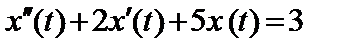
| 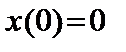  . .
|
11.36. 
|  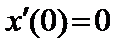 . .
|
11.37. 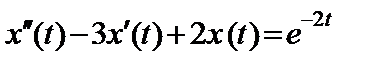
|   . .
|
11.38. 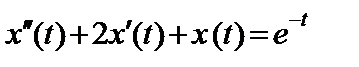
|   . .
|
11.39. 
|   . .
|
11.40. 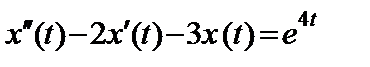
|  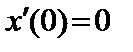 . .
|
 2017-10-25
2017-10-25 502
502








