Дифференциальные операции первого порядка

1) Умножая вектор на скалярную функцию , получим :

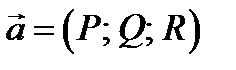2) Скалярное произведение вектора на вектор-функцию даёт: .

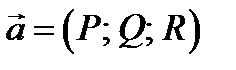3) Векторное произведение вектора на вектор-функцию даёт :

Применять оператор нужно, соблюдая следующие правила:

1) Линейность оператора . Пусть - вещественные или комплексные числа, - скалярные или векторные функции. Тогда

2) Действие оператора на произведение функций. .

(Символ «↓» указывает на объект действия оператора).

Докажем, например, что .

.

При доказательстве воспользовались свойством смешанного произведения векторов .