Пусть в области G заданы скалярное поле 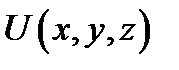 и векторное поле
и векторное поле 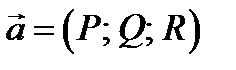 , такие, что функции
, такие, что функции 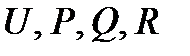 имеют в области G непрерывные частные производные второго порядка. Тогда
имеют в области G непрерывные частные производные второго порядка. Тогда 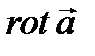 и
и 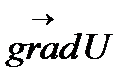 - дифференцируемые векторные поля,
- дифференцируемые векторные поля, 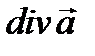 - дифференцируемое скалярное поле. В этих случаях к полям
- дифференцируемое скалярное поле. В этих случаях к полям 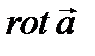 и
и 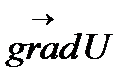 применимы операции вычисления дивергенции и ротора, а к полю
применимы операции вычисления дивергенции и ротора, а к полю 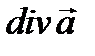 - операция вычисления градиента. Таким образом, получим пять повторных операций:
- операция вычисления градиента. Таким образом, получим пять повторных операций:
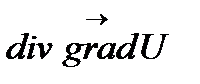 ,
, 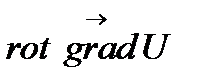 ,
, 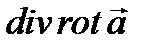 ,
, 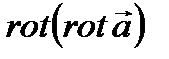 ,
, 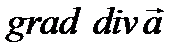 .
.
Определение. Операция 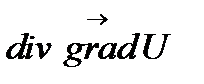 называется оператором Лапласа и обозначается символом
называется оператором Лапласа и обозначается символом  (лапласиан):
(лапласиан): 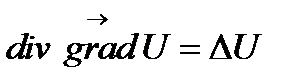 . Оператор Лапласа можно записать с помощью оператора набла
. Оператор Лапласа можно записать с помощью оператора набла  :
:
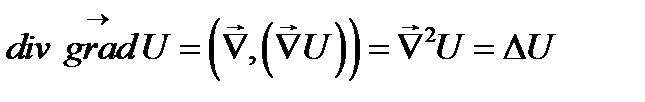 .
.
При этом 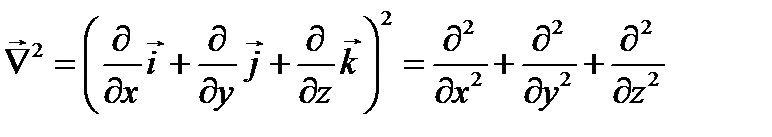 .
.
Тогда 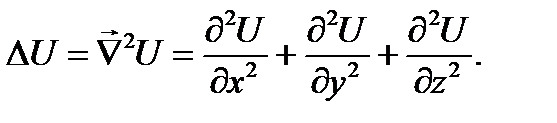
Определение. Уравнение в частных производных 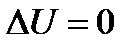 или
или 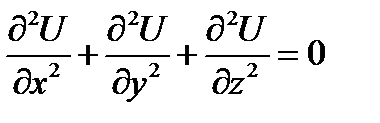 называют уравнением Лапласа.
называют уравнением Лапласа.
Дважды дифференцируемую функцию 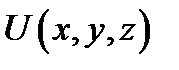 , удовлетворяющую этому уравнению, называют гармонической в области G. Для плоской области уравнение Лапласа примет вид:
, удовлетворяющую этому уравнению, называют гармонической в области G. Для плоской области уравнение Лапласа примет вид: 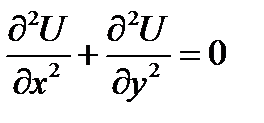 .
.
Примеры гармонических функций: 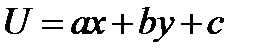 ,
, 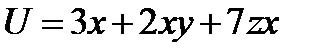 ,
, 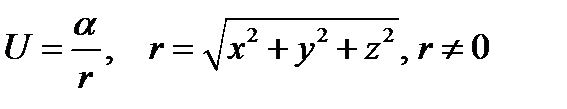 .
.
 2017-11-01
2017-11-01 399
399








