2017-11-01
2257
Пусть в области G, ограниченной поверхностью σ, задано векторное поле 
. 
- единичный вектор внешней нормали к поверхности σ в точке М. Пусть функции 
и их частные производные 
непрерывны в замкнутой области G. Тогда справедлива формула Остроградского-Гаусса:
(14.11)
Или: 
По этой формуле поверхностный интеграл 2-ого рода преобразуется в тройной интеграл.
Векторная форма записи этой формулы: 
. (14.12)
Физический смысл формулы Остроградского-Гаусса: для того, чтобы поток векторного поля в сторону внешней нормали был отличен от нуля, внутри области G должны быть источники или стоки поля. Но тогда 
будет отлична от нуля. Само векторное поле как бы расходится от источников. Отсюда происходит название «дивергенция», или «расходимость».
Из формулы Остроградского-Гаусса следует, что в объёмно односвязной области поток соленоидального поля через любую замкнутую поверхность, расположенную в этой области, равен нулю. Для объёмно неодносвязной области поток может и не быть равным нулю. Слово «соленоидальное» обозначает «трубчатое». Для соленоидального поля имеет место закон сохранения интенсивности векторной трубки, который заключается в следующем: в соленоидальном векторном поле 
поток через любое сечение векторной трубки имеет одно и то же значение. 
.
Пример 14.3. Найдём дивергенцию векторного поля 
и исследуем расположение источников и стоков.
Решение. По формуле (14.10): 
.
, если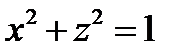 
.
Это уравнение цилиндра
(см. рис.14.4). Внутри цилиндра в области 
расположены стоки поля 
. Вне цилиндра 
расположены источники поля 
. На самом цилиндре нет ни источников, ни стоков.
| Рисунок 14.4 |
Пример 14.4. Найдём поток векторного поля 
через полную поверхность сферы 
.
Решение. Поток векторного поля через поверхность 
. Так как поверхность замкнута, его можно вычислить по формуле
| Рисунок 10 |
| Рисунок 14.5 |
. Тогда 
. Учитывая смещение сферы по оси OX, перейдём к сферическим координатам: (см. рис.14.5) 
, 
.
Уравнение сферы при этом примет вид: 
. Составим интеграл в новых координатах и расставив пределы интегрирования в повторном интеграле, вычислим его.
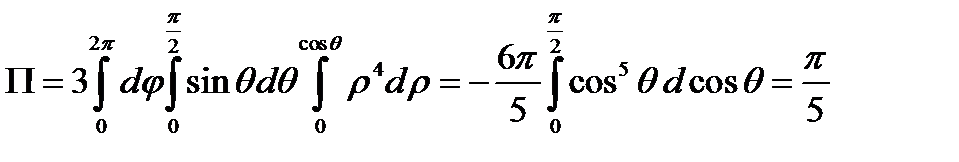. Ответ: 
.
| Рисунок 11 |
через часть поверхности эллипсоида 
, 
в направлении, составляющем тупой угол с OZ, используя формулу Остроградского – Гаусса. | Рисунок 14.6 |
Решение. Рассмотрим следующий способ решения. Достроим данную поверхность до замкнутой, «замкнув» её координатными плоскостями 
. (См. рис.14.6) По свойству аддитивности поверхностного интеграла, поток П через замкнутую поверхность есть сумма потоков через часть эллипсоида и через части координатных
плоскостей. Тогда 
.
Функции 
непрерывны вместе со своими частными производными во всех точках 
. Поток векторного поля через полную поверхность замкнутого тела вычислим по формуле (14.12)
, где 
, т.е.
.
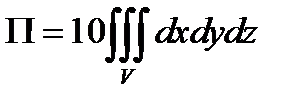Если учесть, что 
- объём одной восьмой части тела, ограниченного эллипсоидом то получаем 
.
Потоки через части координатных плоскостей, замыкающих наше тело, вычисляем по формуле (14.7), у читывая направления нормальных векторов.
, т. к. 
;
, т. к. 
;
, т. к. 
. И учитывая, что , получаем ответ: 
.
Занятие 15.
Теория: Криволинейный интеграл в векторном поле и условия его независимости от пути интегрирования. Потенциальное векторное поле, его свойства. Циркуляция и ротор векторного поля. Формула Стокса и ее применение. Оператор Лапласа. Гармонические поля.
ОЛ-1 гл.5,6,7,8, ОЛ-4 гл.3, ОЛ-4 § 12 п.12.4.
Практика: ОЛ-6 №№ 2398 в), 2355, 2356, 2360 или ОЛ-5 №№ 10.110, 113, 116, 121, 150
Домашнее задание к занятию 15: ОЛ-6 №№ 2357, 2358, 2359, 2397
