| Рисунок 15.1 |
 Криволинейный интеграл векторного поля – это криволинейный интеграл второго рода. Определяется он следующим образом. Пусть в области G задано векторное поле
Криволинейный интеграл векторного поля – это криволинейный интеграл второго рода. Определяется он следующим образом. Пусть в области G задано векторное поле  и в этом поле определена гладкая или кусочно-гладкая ориентированная кривая АВ. Разобьём кривую АВ на n частей точками
и в этом поле определена гладкая или кусочно-гладкая ориентированная кривая АВ. Разобьём кривую АВ на n частей точками  по направлению от А к В. (см. рис.15.1)Радиус-вектор точки
по направлению от А к В. (см. рис.15.1)Радиус-вектор точки  обозначим
обозначим  . Вектор
. Вектор  . Выберем произвольно на каждой частичной дуге
. Выберем произвольно на каждой частичной дуге 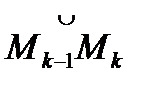 точку
точку  и вычислим вектор поля
и вычислим вектор поля  в них. Для всех
в них. Для всех  вычислим значения скалярного произведения
вычислим значения скалярного произведения  и составим интегральную сумму
и составим интегральную сумму  .
.
Определение. Криволинейным интегралом векторного поля  вдоль дуги АВ называется предел (если он существует), к которому стремится интегральная сумма
вдоль дуги АВ называется предел (если он существует), к которому стремится интегральная сумма  , если наибольшая из длин частичных дуг
, если наибольшая из длин частичных дуг  стремится к нулю, а число элементарных дуг n неограниченно возрастает. Этот предел обозначают символом
стремится к нулю, а число элементарных дуг n неограниченно возрастает. Этот предел обозначают символом  . Т.е.
. Т.е.
 . (15.1)
. (15.1)
При изменении ориентации кривой интеграл меняет знак:  .
.
Физический смысл выражения  - это работа, произведённая силой
- это работа, произведённая силой  при перемещении материальной точки от А к В по линии L.
при перемещении материальной точки от А к В по линии L.
 (15.2)
(15.2)
Криволинейный интеграл векторного поля вдоль замкнутой кривой (контура L) называется циркуляцией поля по замкнутому контуру при заданном направлении обхода контура и обозначается символом
 (15.3)
(15.3)
(знак + обозначает, что контур обходится против часовой стрелки).
Пусть поле задано своими функциями-координатами  и
и  . Тогда
. Тогда
 . (15.4)
. (15.4)
В правой части выражения (15.4) - криволинейный интеграл второго рода.
Для плоского поля 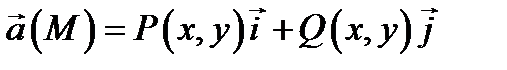 криволинейный интеграл вычисляется по формуле:
криволинейный интеграл вычисляется по формуле:  . (15.5)
. (15.5)
Криволинейный интеграл векторного поля вычисляется по обычным правилам вычисления криволинейного интеграла второго рода, т.е. преобразовывается в определённый. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование. (См. занятие 10)
Пример 15.1. Найдём работу векторного поля  при перемещении точки вдоль меньшей части кривой, являющейся пересечением цилиндра
при перемещении точки вдоль меньшей части кривой, являющейся пересечением цилиндра  и параболоида гиперболического
и параболоида гиперболического  , от точки
, от точки  к
к  .
.
Решение. Построим заданную часть кривой (см. рис. 15.2) и вычислим работу по формуле (15.2):
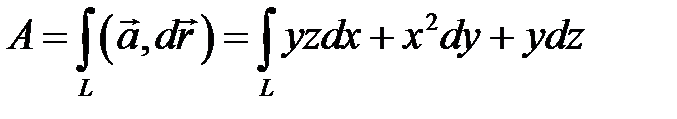 .
.
Построенный криволинейный интеграл 2-ого рода сведём к определённому.
 Для этого используем параметрическую форму записи уравнений кривой
Для этого используем параметрическую форму записи уравнений кривой  , где
, где  .
.
Тогда работа
| Рисунок 15.2 |
 .
.
После вычисления получаем ответ:  .
.
 2017-11-01
2017-11-01 4635
4635
