Плоскость

Приложения.

1) Условие параллельности и перпендикулярности двух прямых.

Даны две прямые 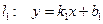и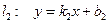

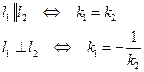
2) Угол между двумя прямыми.

Даны две прямые 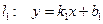и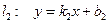

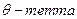— угол между этими прямыми. Тогда

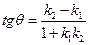
3) Расстояние от точки до прямой.

Дана прямая 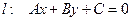и точка не лежащая на этой прямой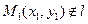

Тогда расстояние от точки 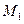до прямой 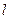вычисляется по формуле

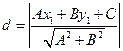
Определение:

Каждую плоскости в пространстве задает уравнение 1-го порядка:

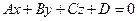, где .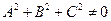

Геометрический смысл коэффициентов.

1) A=0 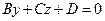, плоскость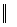

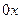
B=0 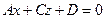, плоскость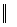

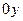
С=0 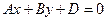, плоскость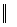

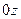
2) А=0, D=0 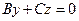, проходит через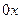

B=0, D=0 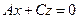, проходит через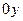

C=0, D=0 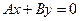, проходит через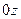

3) A=0, B=0 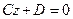, плоскость 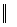плоскости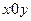

A=0, C=0 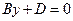, плоскость 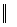плоскости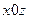

B=0, C=0 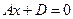, плоскость 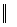плоскости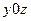

4) A=0, B=0, D=0 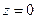плоскость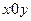

A=0, C=0, D=0 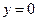плоскость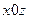

B=0, C=0, D=0 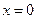плоскость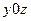

Определение:

Обозначим через 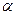некоторую плоскость.

Ненулевой вектор 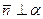называется нормальным вектором плоскости.

Утверждение.

Если точка 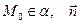— нормальный вектор этой плоскости, то точка

и вектор однозначно задают эту плоскость.