Алгоритмы линейной структуры
Изображение алгоритма в виде блок-схемы
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур - блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала-конца алгоритма (рис. 1.1). Надпись на блоке: "начало" ("конец").
Блок ввода-вывода данных (рис. 1.2). Надпись на блоке: слово "ввод" ("вывод" или "печать") и список вводимых (выводимых) переменных.
 |  |
| Рис. 1.1. Блок начала-конца алгоритма | Рис. 1.2. Блок ввода-вывода данных |
Блок решения или арифметический (рис. 1.3). Надпись на блоке: операция или группа операций.
Условный блок (рис. 1.4). Надпись на блоке: условие. В результате проверки условия осуществляется выбор одного из возможных путей (ветвей) вычислительного процесса. Если условие выполняется, то следующим выполняется этап по ветви "+", если условие не выполняется, то выполняется этап по ветви "–".
 | 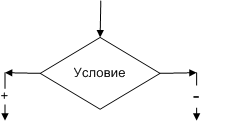 |
| Рис. 1.3. Арифметический блок | Рис. 1.4. Условный блок |
Линейный алгоритм - это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.5).
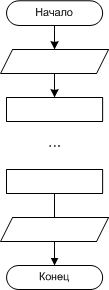 |
| Рис. 1.5 Размещение блоков в линейном алгоритме |
Рассмотрим несколько примеров линейных алгоритмов.
ПРИМЕР 1.1. Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника.
Пусть a, b, c - длины сторон треугольника. Необходимо найти S - площадь треугольника, P - периметр.
Для нахождения площади можно воспользоваться формулой Герона:
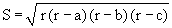 , где r - полупериметр
, где r - полупериметр
Входные данные: a, b, c.
Выходные данные: S, P.
Блок-схема алгоритма представлена на рис. 1.6.
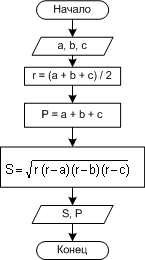 |
| Рис. 1.6. Алгоритм примера 1.1 |
Внимание!!! В этих блоках знак "=" означает не математическое равенство, а операцию присваивания. Переменной, стоящей слева от оператора, присваивается значение, указанное справа. Причем это значение может быть уже определено или его необходимо вычислить с помощью выражения. Например, операция r = (a+b+c)/2 - имеет смысл (переменной r присвоить значение r=(a+b+c)/2), а выражение (a+b+c)/2=r - бессмыслица.
В компьютере такой порядок, что сначала выделяется место, куда будет ставится результат, а потом определяется процесс вычисления, с помощью которого этот результат присваивается.
Пример. Рассмотрим блок схему для жизненной ситуации.
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. В блок-схемах разветвленные алгоритмы изображаются так, как показано на рис. 1.7 - 1.8.
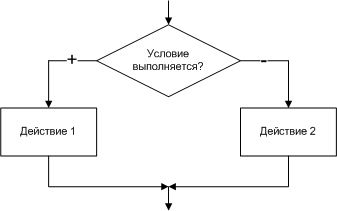 | 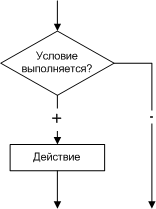 |
| Рис. 1.7. Фрагмент алгоритма | Рис. 1.8. Пример разветвления |
Рассмотрим несколько примеров построения алгоритмов разветвленной структуры.
Пример. Есть детский сад, в котором много детей. Тренер из балетной школы хочет набрать детей в балетную школу. Подойдут только дети не старше трех лет.
Пример. Исследование медицинских данных детей от 7 до 10 лет. (самотоятельно)
Пример. Вычислить y=(a+b)/c, c=a-b
Пример. Вычислить y=(2x+3)/(z-1), z=4-x. (самостоятельно)
ПРИМЕР 1.2. Известны коэффициенты a, b, и с квадратного уравнения. Вычислить корни квадратного уравнения.
Входные данные: a, b, c.
Выходные данные: x1, x2.
d – дискрименант, вычисляется пл формуле.
Все известные в школе формулы и все вычислительные процедуры высшей математики (интегралы, sin и т.д.), запрограммировано в компьютере.
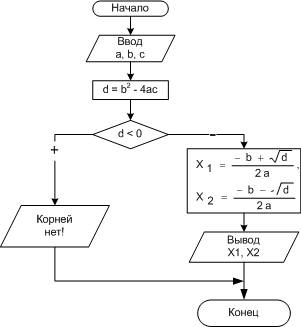 |
| Рис. 1.9. Алгоритм решения квадратного уравнения |
Если d<0, нельзя извлекать корень из отрицательного числа.
ПРИМЕР 1.3. Найти наибольшее из трех чисел.
Входные данные: a, b, c.
Выходные данные: m.
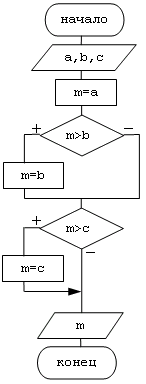
| Рис. 1.10. Алгоритм примера 1.3 |
Пояснения к блок-схеме: вводится дополнительная переменная m, в которой хранится текущее значение наибольшего (максимального) числа. Далее каждое следующее число сравнивается с переменной m и если значение сравниваемого числа оказывается больше, то оно запоминается в переменную m.
ПРИМЕР 1.4. Модель платья окрашена в три базовых цвета: красный, синий, зеленый. Подсчитать частоту встречаемости каждого цвета в модели.
Каждый цвет закодирован: красный – 1, синий – 2, зеленый – 3.
Входные данные: cvet
Выходные данные kol_red, kol_blue, kol_green
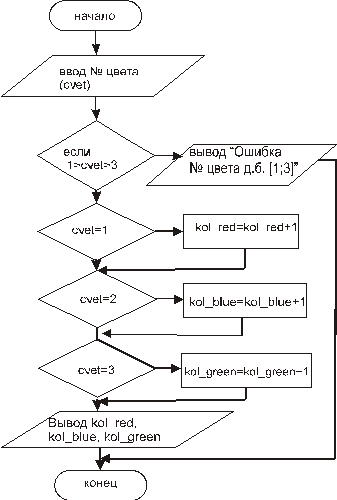
Рис. 1.11. Алгоритм примера 1.4.
 2013-12-28
2013-12-28 2639
2639








