Аксиоматика создаваемой теории мотивационного поведения потребителей предполагает:
- представительное количество потребителей 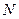 пространстве мотивации их поведения;
пространстве мотивации их поведения;
- равномерность распределения потребителей в информационном поле этого пространства;
- «стационарность» движения потребителей в пространстве мотивации их поведения, при этом, сущность поведения характеризуется мысленным назначением потребителем своей индивидуальной цены на товар;
- «стационарность» в процессе движении достаточно большого количества потребителей 
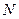 , характеризующаяся тем, что при выделении любой, даже бесконечно малой области пространства, количество потребителей
, характеризующаяся тем, что при выделении любой, даже бесконечно малой области пространства, количество потребителей 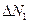 , покидающих эту область пространства, равно количеству потребителей
, покидающих эту область пространства, равно количеству потребителей 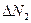 , входящих в указанную ту же область, то есть
, входящих в указанную ту же область, то есть
Более строгая математическая интерпретация вывода распределения приведена ниже:
Исходя из представительного количества потребителей 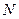 в пространстве мотивации поведения, равномерности распределения потребителей в информационном поле этого пространства; «стационарности» движения потребителей в пространстве мотивации их поведения, «стационарности» процесса движения достаточно большого количества потребителей
в пространстве мотивации поведения, равномерности распределения потребителей в информационном поле этого пространства; «стационарности» движения потребителей в пространстве мотивации их поведения, «стационарности» процесса движения достаточно большого количества потребителей 
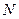 , характеризующейся тем, что при выделении любой, даже бесконечно малой области пространства, количество потребителей
, характеризующейся тем, что при выделении любой, даже бесконечно малой области пространства, количество потребителей 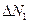 , покидающих эту область пространства, равно количеству потребителей
, покидающих эту область пространства, равно количеству потребителей 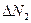 , входящих в указанную ту же область, можно предположить, что
, входящих в указанную ту же область, можно предположить, что
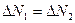 . (2.1)
. (2.1)
Следуя далее (5) можно считать, что в любом месте предполагаемого теорией пространства и при любом выбранном конечном числе потребителей, (модельно представимых в виде точек пространства), осуществляют воздействия большое количество равнозначных факторов: это вторичное предположение вытекает из свойства «стационарности» рассматриваемого процесса при наличии в нём достаточно большого количества потребителей-объектов.
Последнее предположение определённо указывает о действии между потребителями нормального закона распределения [48], который, прежде всего, должен проявить себя в закономерности поведения скоростного параметра в виде мотивируемых каждым потребителем цен 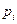 на товар, поскольку причиной, способствующей мотивации именно указанной цены на товар, являются воздействия на материальные точки-потребители многочисленных и сравнительно равновеликих факторов.
на товар, поскольку причиной, способствующей мотивации именно указанной цены на товар, являются воздействия на материальные точки-потребители многочисленных и сравнительно равновеликих факторов.
Используя в качестве оценки цены бесконечно малое изменение параметра нормального распределения Гаусса, примем, что
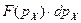 - (2.2)
- (2.2)
- это вероятность того, что некоторый покупатель-точка в некоторый момент времени в пространстве мотивации имеет проекцию на ось 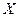 мотивируемой им цены
мотивируемой им цены 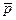 на товар в интервале значений от
на товар в интервале значений от 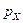 до
до 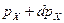 .
.
При этом остальные две проекции цены 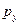 и
и 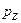 первоначально не рассматриваются [285, 131, 95, 394]. Тогда, как известно из теории вероятностей [48, 243] и теории распределений [128, 130, 285], функция
первоначально не рассматриваются [285, 131, 95, 394]. Тогда, как известно из теории вероятностей [48, 243] и теории распределений [128, 130, 285], функция 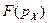 характеризует плотности распределения вероятностей мотивируемых потребителями цен, и поэтому для нормального распределения Гаусса можно записать:
характеризует плотности распределения вероятностей мотивируемых потребителями цен, и поэтому для нормального распределения Гаусса можно записать:
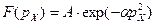 , (2.3)
, (2.3)
где
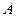 и
и 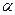 - параметры распределения, причём
- параметры распределения, причём 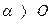 .
.
Если просуммировать все значения плотности распределения при теоретически допустимых значениях 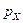 от
от 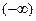 до
до 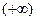 , что характеризует реально два предельных случая мотивационного поведения потребителей, то: первый случай - это когда потребитель, (в силу ряда причин, связанных с ненужностью товара или с неудовлетворённым разочарованием, что товар невозможно приобрести потребителю в данное время), отказывается вообще назначать товару мотивированную цену; второй противоположный случай - это когда потребитель в силу своего незнания или невежества, характеризующихся незнанием товара или его потребительских свойств, назначают за этот товар фантастично большую цену.
, что характеризует реально два предельных случая мотивационного поведения потребителей, то: первый случай - это когда потребитель, (в силу ряда причин, связанных с ненужностью товара или с неудовлетворённым разочарованием, что товар невозможно приобрести потребителю в данное время), отказывается вообще назначать товару мотивированную цену; второй противоположный случай - это когда потребитель в силу своего незнания или невежества, характеризующихся незнанием товара или его потребительских свойств, назначают за этот товар фантастично большую цену.
Используя перечисленные случаи поведения потребителей и пронормировав к единице предельную (от 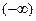 до
до 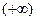 ) сумму величин плотностей распределения, можно записать значение интеграла плотности в следующем виде:
) сумму величин плотностей распределения, можно записать значение интеграла плотности в следующем виде:
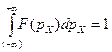 . (2.4)
. (2.4)
Интеграл (2.4) позволяет получить выражение для 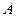 в общем виде, используя (7):
в общем виде, используя (7):
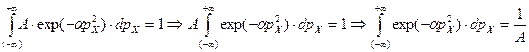 (2.5)
(2.5)
Интеграл (2.5) достаточно широко известен в математике и имеет собственное название как интеграл Пуассона [131, 285], который равен 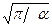 . Тогда
. Тогда
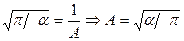 . (2.6)
. (2.6)
Подставив (2.6) в (2.5), получаем выражение для плотности распределения, имеющее уже один параметр 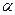 в распределении:
в распределении:
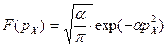 . (2.7)
. (2.7)
Аналогичным образом представляется возможность описать функции плотностей вероятностей 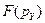 и
и 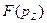 для проекций цен соответственно на оси
для проекций цен соответственно на оси 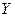 и
и 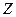 , повторив аналогичный вывод распределения.
, повторив аналогичный вывод распределения.
Если теперь обобщить плотность вероятности таким образом, чтобы обеспечить прогнозный учёт мотивируемой потребителем цены в проекциях 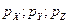 на все три пространственные оси, то необходимо применить теорему умножения вероятностей, учитывая при этом, в силу независимости координатных осей друг от друга, также независимость и проекций вектора цены на эти оси [48]. Тогда:
на все три пространственные оси, то необходимо применить теорему умножения вероятностей, учитывая при этом, в силу независимости координатных осей друг от друга, также независимость и проекций вектора цены на эти оси [48]. Тогда:
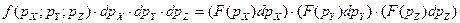 . (2.8)
. (2.8)
Как уже отмечалось, выражение (12) справедливо, если события независимы, что согласуется с первоначальным допущением об однородности и изотропности введенного нами пространства с координатными осями 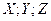 . Следовательно:
. Следовательно:
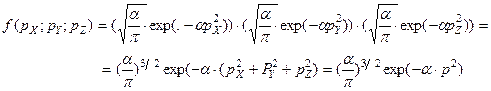 , (2.9)
, (2.9)
где
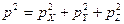 - квадрат прогнозируемой цены (модуль). (2.10)
- квадрат прогнозируемой цены (модуль). (2.10)
Из (2.10) следует, что плотность совместной вероятности проекций цены на оси 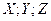 должны соответствовать квадратичной формуле (14). И это закономерно, поскольку различные направления векторов мотивируемых цен (как скоростных параметров) равновероятны, так что плотность вероятности может зависеть только от модуля вектора цены, который (модуль) мотивированно прогнозировал потребитель. Поэтому вероятность проявления прогнозируемой цены каким-нибудь потребителем с проекциями этой цены
должны соответствовать квадратичной формуле (14). И это закономерно, поскольку различные направления векторов мотивируемых цен (как скоростных параметров) равновероятны, так что плотность вероятности может зависеть только от модуля вектора цены, который (модуль) мотивированно прогнозировал потребитель. Поэтому вероятность проявления прогнозируемой цены каким-нибудь потребителем с проекциями этой цены
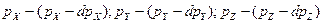 (2.11)
(2.11)
составит в соответствии с (13):
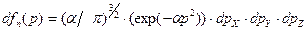 , (2.12)
, (2.12)
где 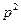 соответствует (10).
соответствует (10).
Дальнейшие исследования связаны с учётом равновероятных направлений векторов мотивируемых цен в пространстве мотивационного поведения потребителей при условии: вероятность нахождения потребителя ограничивается значениями модулей цены в пределах от 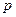 до
до 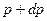 . При этом направления векторов цен, мотивируемых большим количеством покупателей равновероятно распределены по всем направлениям: поэтому основное влияние на плотность распределения оказывает только модуль цены
. При этом направления векторов цен, мотивируемых большим количеством покупателей равновероятно распределены по всем направлениям: поэтому основное влияние на плотность распределения оказывает только модуль цены 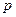 .
.
Тогда можно оценить вероятность присутствия (выявления) покупателя, обозначенной как 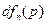 , обычным подсчётом частоты проявления [48, 285] в виде:
, обычным подсчётом частоты проявления [48, 285] в виде:
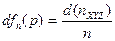 , (2.13)
, (2.13)
где 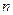 - число потребителей в объёме элементарного пространства мотивации поведения в виде
- число потребителей в объёме элементарного пространства мотивации поведения в виде 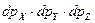 (рис. 4 -1,а);
(рис. 4 -1,а);
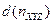 - количество потребителей, мотивирующих цену
- количество потребителей, мотивирующих цену 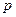 в пределах элементарного пространства
в пределах элементарного пространства 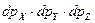 (рис. 4 - 1,а).
(рис. 4 - 1,а).
Тогда (16) возможно записать с учётом (17):
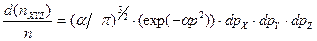 (2.14)
(2.14)
Наличие элементарного объёма пространства мотивации в (18) не позволяет применить полученную закономерность (2.14) для практического использования. Поэтому, используя равную вероятность [285, 95] направлений многочисленных векторов-цен, мотивируемых потребителями, осуществим переход от декартовой системы координат к полярной, позволяющей за счёт введения радиуса вектора цены и трансформируя угол поворота этого радиуса вектора избежать присутствие параметров и зависимость от них элементарного объёма 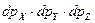
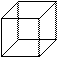
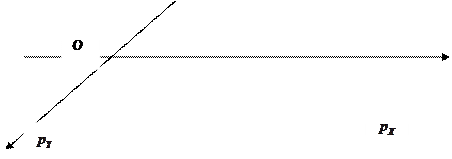
Рассмотрим элементарный объём 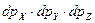 в декартовой системе координат
в декартовой системе координат 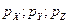 (рис. 1,а). Поскольку указанный элементарный объём бесконечно мал, форма его может быть принципиально любой: тогда традиционное представление элементарного объёма в виде куба однозначно может быть заменено элементарным шаром, положение в пространстве которого, (в силу его (шара) бесконечно малых размеров), однозначно может быть определено радиус-вектором его цены
(рис. 1,а). Поскольку указанный элементарный объём бесконечно мал, форма его может быть принципиально любой: тогда традиционное представление элементарного объёма в виде куба однозначно может быть заменено элементарным шаром, положение в пространстве которого, (в силу его (шара) бесконечно малых размеров), однозначно может быть определено радиус-вектором его цены 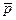 и углом
и углом 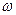 , отсчитанным от принятого направления ориентации (рис. 1, б).
, отсчитанным от принятого направления ориентации (рис. 1, б).
|
|
|
|


 а)
а)
|
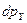

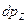
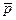
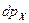
 | |||||
 | |||||
|
б) 

|
 в)
в)
 | |||
 |
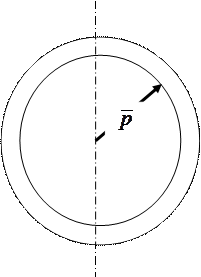
При таком преобразовании элементарного объёма представляется далее множественное вращение радиуса-вектора 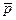 по абсолютно всем направлениям в пространстве, что приведёт как бы к образованию из элементарного объёма шара своеобразной шаровой полой и утончённой поверхности, толщина которой
по абсолютно всем направлениям в пространстве, что приведёт как бы к образованию из элементарного объёма шара своеобразной шаровой полой и утончённой поверхности, толщина которой 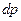 (рис.1,в) также бесконечно мала, поскольку значительно меньше радиуса принятого нами элементарного объёма шара, размеры которого оцениваются как бесконечно малые. При этом радиус шаровой поверхности определяется модулем радиуса-вектора
(рис.1,в) также бесконечно мала, поскольку значительно меньше радиуса принятого нами элементарного объёма шара, размеры которого оцениваются как бесконечно малые. При этом радиус шаровой поверхности определяется модулем радиуса-вектора 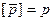 (рис.1, в).
(рис.1, в).
Если обозначить [128, 131, 285, 166] бесконечно малый объём шарового слоя через 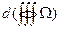 , то, используя принцип сравнимости бесконечно малых величин одной размерности, можно записать, что
, то, используя принцип сравнимости бесконечно малых величин одной размерности, можно записать, что
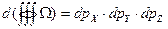 . (2.15)
. (2.15)
Подставив (19) в (18), получим:
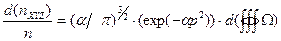 . (2.16)
. (2.16)
Тогда объём шарового слоя можно определить при бесконечно малой его толщине 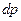 как
как
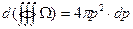 . (2.17)
. (2.17)
Если обозначить 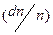 - вероятность того, что у произвольно выбранного покупателя мотивированная им цена окажется в пределах между
- вероятность того, что у произвольно выбранного покупателя мотивированная им цена окажется в пределах между 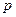 и
и 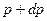 , что соответствует частоте
, что соответствует частоте 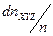 , то (20) можно записать с учётом (21):
, то (20) можно записать с учётом (21):
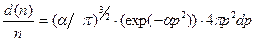 (2.18)
(2.18)
или
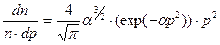 , (2.19)
, (2.19)
где
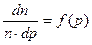 - (2.20)
- (2.20)
- функция распределения потребителей по мотивируемым ими ценам как отношение: вероятности наличия потребителей, назначивших цену в пределах от 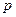 до
до 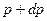 (числитель), к изменению мотивируемой цены (знаменатель); данная функция распределения характеризует плотность вероятностей мотивируемого назначения потребителями различных цен.
(числитель), к изменению мотивируемой цены (знаменатель); данная функция распределения характеризует плотность вероятностей мотивируемого назначения потребителями различных цен.
Подставив (2.19) в (2.20), получаем окончательно функцию искомого распределения:
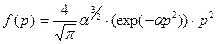 , (2.21)
, (2.21)
где
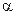 - параметр распределения.
- параметр распределения.
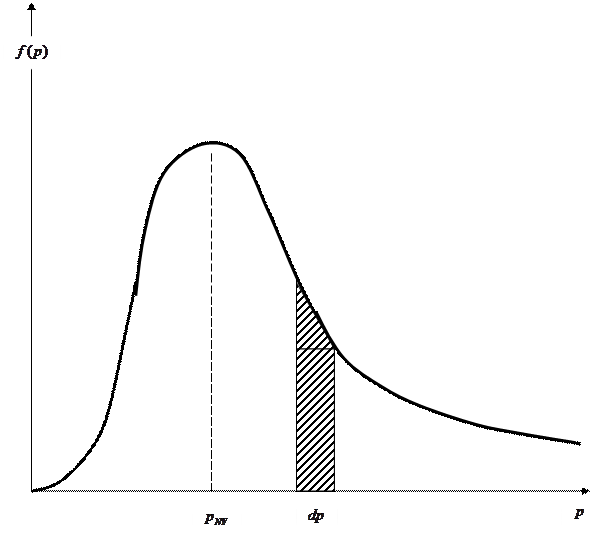
Графически функция 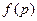 распределения потребителей согласно мотивируемым ими ценам на товар представлена на рис. 4.2. Как и предполагалось исходными условиями вывода распределения, полученная функция распределения обращается в нуль при мотивированной потребителем цене
распределения потребителей согласно мотивируемым ими ценам на товар представлена на рис. 4.2. Как и предполагалось исходными условиями вывода распределения, полученная функция распределения обращается в нуль при мотивированной потребителем цене 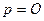 и при цене
и при цене 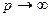 , то есть когда потребитель, соответственно, отказывается от мотивированной оценке товара, или, когда потребитель проявляет полную некомпетентность и абсолютное безразличие к данному товару, назначая фантастически большую цену. Как видно из рис.2., функция распределения имеет максимум при некотором значении мотивируемой цены
, то есть когда потребитель, соответственно, отказывается от мотивированной оценке товара, или, когда потребитель проявляет полную некомпетентность и абсолютное безразличие к данному товару, назначая фантастически большую цену. Как видно из рис.2., функция распределения имеет максимум при некотором значении мотивируемой цены 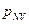 . С позиций мотивационного поведения потребителей наличие максимума означает, что наибольшая доля всех потребителей мотивирует назначаемые ими цены в пределах, достаточно близких к определённой цене
. С позиций мотивационного поведения потребителей наличие максимума означает, что наибольшая доля всех потребителей мотивирует назначаемые ими цены в пределах, достаточно близких к определённой цене 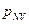 . В ряде случаев указанная цена
. В ряде случаев указанная цена 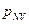 близка к рыночной цене товара, однако последнее не обязательно, что, прежде всего, относится к вновь осваиваемым товарам, связанным на этапе освоения с инновационными издержками, или к прочим дефицитным товарам, цены на которые за счёт их дефицитности неоправданно завышены; имеются и другие причины несоответствия рыночных цен ценам
близка к рыночной цене товара, однако последнее не обязательно, что, прежде всего, относится к вновь осваиваемым товарам, связанным на этапе освоения с инновационными издержками, или к прочим дефицитным товарам, цены на которые за счёт их дефицитности неоправданно завышены; имеются и другие причины несоответствия рыночных цен ценам 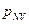 (снижение жизненного уровня большинства населения, демографические факторы).
(снижение жизненного уровня большинства населения, демографические факторы).
Анализ функционального выражения полученного распределения показывает, что мотивированные цены, близкие к 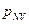 , статистически мотивировано объявляются потребителями чаще других цен; поэтому можно сказать, что вероятность того, что мотивировано объявляемая цена потребителем близкая к
, статистически мотивировано объявляются потребителями чаще других цен; поэтому можно сказать, что вероятность того, что мотивировано объявляемая цена потребителем близкая к 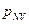 будет
будет
 | |||||
| |||||
наибольшая. Поэтому мотивируемую цену, при которой полученное распределение вероятности мотиваций потребителей будет максимальной,.
 2014-01-25
2014-01-25 733
733

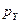
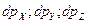 и объемом
и объемом 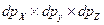 ; б) в виде «элементарного» бесконечно малого объёма шара; в) в виде шарового слоя с бесконечно его толщиной и конечным радиусом
; б) в виде «элементарного» бесконечно малого объёма шара; в) в виде шарового слоя с бесконечно его толщиной и конечным радиусом 






