Понятие общего решения

Если для уравнения первого порядка общее решение содержит одну произвольную постоянную, то для уравнения п - го порядка общее решение зависит от п произвольных постоянных: .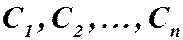

Определение. Функция 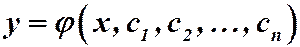называется общим решением уравнения (1), если выполняются два условия:

1) эта функция удовлетворяет уравнению (1) при любых значениях постоянных ;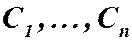

2) При заданных начальных условиях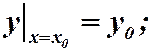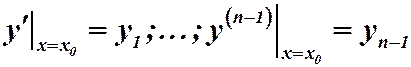постоянные 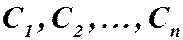можно подобрать таким образом, чтобы эти начальные условия выполнялись.

Понятие частного решения уравнения

Определение. Частным решением уравнения (1) называется любое его решение, которое получается из общего при конкретных значениях постоянных .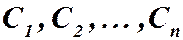

Простейшим уравнением п -го порядка является уравнение: .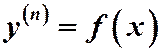

Его общее решение находится путем п - кратного последовательного интегрирования обеих частей уравнения.

Пример.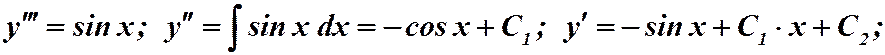

.

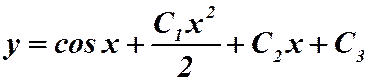7. Уравнения, допускающие понижения порядка

Одним из основных методов интегрирования дифференциальных уравнений высших порядков является метод понижения порядка уравнения.

Рассмотрим на примере уравнения второго порядка: 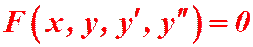(1)

Случай I. Пусть левая часть уравнения (1) не содержит явно искомой функции, т.е. не содержит у и имеет вид: 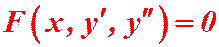(2)

В этом случае понижение порядка производится с помощью подстановки:

.

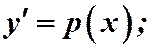
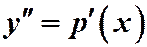Подставляя 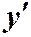и 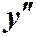в (2) порядок понизится.

Пример 1. 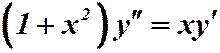. Замена: .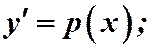

.

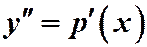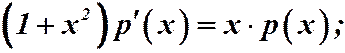
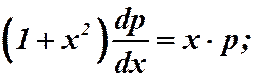
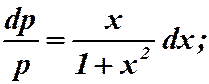
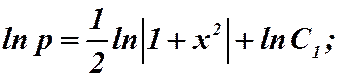
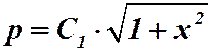Обратная замена: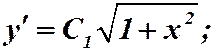

.

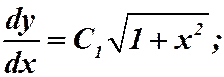
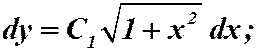
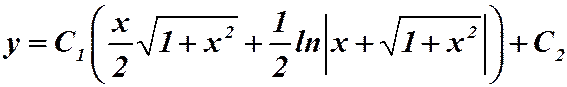Случай II. Пусть левая часть уравнения (1) не содержит явно независимую переменную х, т.е. 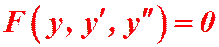(3)

Тогда понижение порядка достигается подстановкой .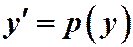

Дифференцирование этого равенства по х производится по правилу сложной функции, т.е. 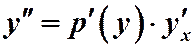, но 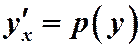, следовательно, 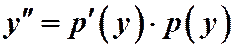, тогда .

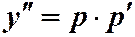Пример 2. .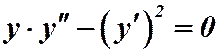

Решение. Замена: , .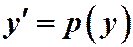

.

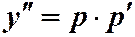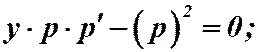
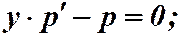
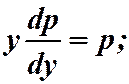
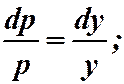
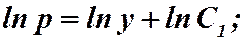
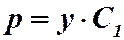Обратная замена: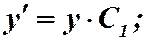

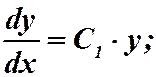
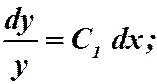
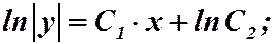
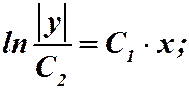. Ответ: .

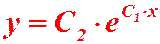Случай III. Промежуточный интеграл.

Может оказаться так, что левая часть уравнения (1) является полной производной по х от некоторого выражения 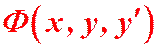, т.е.

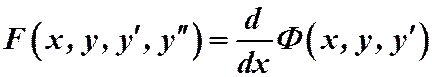. Тогда уравнение принимает вид:

.

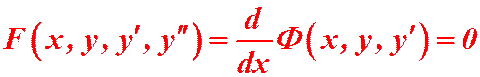Интегрируя обе части уравнения, найдем промежуточный интеграл, при этом порядок уравнения понизится на единицу.

Пример 3. .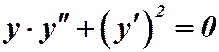

Решение. Выпишем левую часть отдельно:

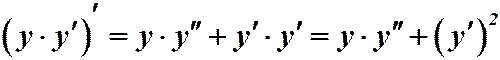, т.е. получаем: .

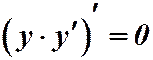Интегрируя, находим:

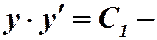это есть промежуточный интеграл;

.

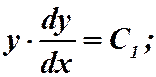
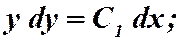
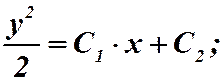
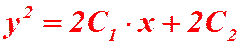8. Линейные дифференциальные уравнения высших порядков

Определение. Дифференциальное уравнение называется линейным, если оно первой степени относительно искомой функции и его производных.

Определение. Линейным неоднородным дифференциальным уравнением п - го порядка называется уравнение вида:

,

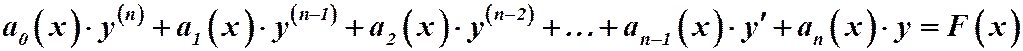где функции 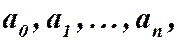называемые коэффициентами, и функция 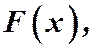называемая правой частью уравнения, определены в некотором интервале .

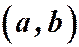Если 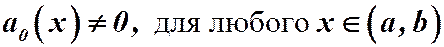, то поделив всё уравнение на 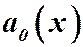, получим: 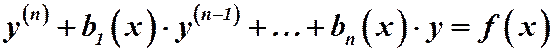(1)

где ; .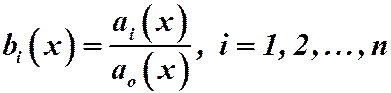

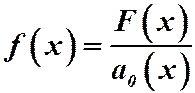Если 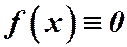, то получим уравнение: 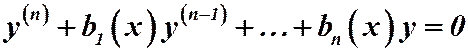(2), которое называется линейным однородным уравнением, соответствующим данному неоднородному уравнению (1).

Например, дано уравнение 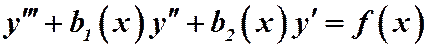. Однородным будет: .

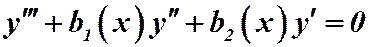9. Свойства решений линейного однородного уравнения