Теория вероятностей – это раздел математики, в котором изучаются теоретические модели опытов со случайными исходами. Эти опыты полностью характеризуются наборами всех возможных их исходов 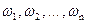 . Понятие исхода опыта является первичными и не определяется. Множество всех исходов данного опыта мы будем обозначать буквой
. Понятие исхода опыта является первичными и не определяется. Множество всех исходов данного опыта мы будем обозначать буквой  :
: 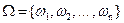 .
.
Определение1. Любое подмножество множества 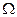 называется событием.
называется событием.
Само множество 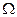 при этом называется достоверным событием и его пустое подмножество
при этом называется достоверным событием и его пустое подмножество 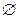 называется невозможным событием.
называется невозможным событием.
Пример А={Выпадение не более шести очков при бросании одной игральной кости}- достоверное событие.
В={Появление 12 очков при бросании одной игральной кости}-невозможное событие.
Если исход 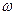 принадлежи событию А, то мы будем говорить также, что исход
принадлежи событию А, то мы будем говорить также, что исход 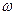 благоприятствует событию А. Согласно данному определению все исходы
благоприятствует событию А. Согласно данному определению все исходы 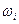 являются элементарными событиями, а все множество -
являются элементарными событиями, а все множество - 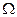 пространством элементарных событий.
пространством элементарных событий.
Пример 1. При бросании монеты возможны 2 элементарных исходов (событий):

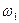 - выпадение орла
- выпадение орла
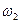 - выпадение решки,
- выпадение решки,
т.е. пространство элементарных событий 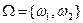
Пример 2. При бросании игральной кости возможны следующие элементарные исходы: 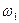 - выпадение 1 очка,
- выпадение 1 очка, 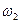 - выпадение 2 очков,
- выпадение 2 очков, 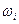 - выпадение i- очков,
- выпадение i- очков, 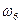 - выпадение 6 очков. Т.е. пространство элементарных событий
- выпадение 6 очков. Т.е. пространство элементарных событий 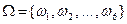 . Событие А, состоящее в выпадении четного числа очков есть
. Событие А, состоящее в выпадении четного числа очков есть 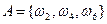 .
.
Определение 2. Событие А влечет за собой событие В, если всякий исход, принадлежащий событию А, принадлежит и событию В и пишут 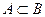 .
.
Определение 3. Два события А и В называются равными, если они состоят из одних и тех же исходов. А = В.
Определение 4. Событие 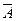 , состоящее из всех исходов
, состоящее из всех исходов 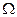 , не принадлежащих событию А, называется противоположным событию А.
, не принадлежащих событию А, называется противоположным событию А.
Определение 5. Суммой двух событий А и В называется событие, состоящее из исходов 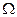 принадлежащих либо событию А либо событию В, обозначается таким образом:
принадлежащих либо событию А либо событию В, обозначается таким образом: 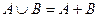 . - (Появление хотя бы одного из этих событий А и В).
. - (Появление хотя бы одного из этих событий А и В).
Пример1. Опыт состоит в пяти выстрелах по мишени. Тогда могут произойти следующие события:
А0- ни одно попадание; А1 – ровно одно попадание; А2 – ровно два попадания;
А3 – ровно три попадания; А4 – ровно четыре попадания; А5 – ровно пять попаданий;
А = А0+ А1+ А2- есть событие «не более двух попаданий»;
В= А3+ А4+ А5 – есть событие «не менее трех попаданий».
Пример2. А – попадание в цель при первом выстреле; В – попадание в цель при втором выстреле, тогда А+В – попадание в цель вообще, безразлично при каком выстреле.
Определение 6. Разностью двух событий А и В называется событие, состоящее из всех исходов принадлежащих событию А и не принадлежащих событию В. 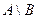 = А – В.
= А – В.
Определение 7. Произведением двух событий А и В называется событие, состоящее из исходов принадлежащих и событию А и событию В одновременно, обозначается таким образом: 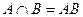 .
.
Пример 1. А – появление туза при вынимании карты из колоды, событие В – появление карты бубновой масти, то событие АВ – есть событие появление бубнового туза.
Пример 2. Пусть производятся два выстрела по мишени. А – попадение при первом выстреле, В – попадение при втором выстреле. То АВ – попадение при обоих выстрелах.
Определение 8. Два события А и В называются несовместными, если они не имеют общих исходов, т.е. 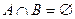 .
.
Введенные операции обладают следующими свойствами:
1. 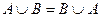 - переместительный закон,
- переместительный закон,
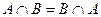 -
-
2. 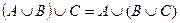
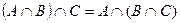
3. 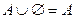
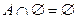
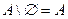
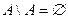
4. 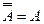
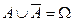
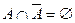
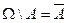
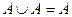
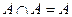
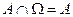
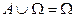
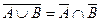
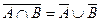
5. 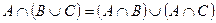
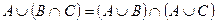
Система событий 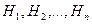 называется полной группой событий, если она осуществляет разбиение пространства
называется полной группой событий, если она осуществляет разбиение пространства 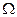 на попарно непересекающиеся события, удовлетворяющие следующим условиям:
на попарно непересекающиеся события, удовлетворяющие следующим условиям:
1) 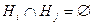 при
при 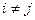 ;
;
2) 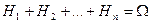 .
.
Пусть 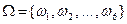 - пространство элементарных событий, соответствующее эксперименту с однократным подбрасыванием игральной кости. Тогда оно может быть разбито, например, на следующие полные группы событий:
- пространство элементарных событий, соответствующее эксперименту с однократным подбрасыванием игральной кости. Тогда оно может быть разбито, например, на следующие полные группы событий:
1) 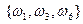
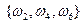
2) 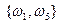
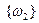
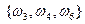
 2014-01-25
2014-01-25 1150
1150
