Теплоемкость

Теплоемкость определяет «температурную инерционность» системы.

.

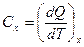X - условия теплообмена. Удельные теплоемкости

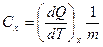- массовая удельная теплоемкость

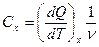- мольная удельная теплоемкость.[12]

В справочной литературе обычно приводятся значения теплоемкостей при постоянном объеме C_V и постоянном давлении C_P. Величина теплоемкости может быть любой (положительной, отрицательной, нулевой, бесконечной). Величина определяется условиями теплообмена.

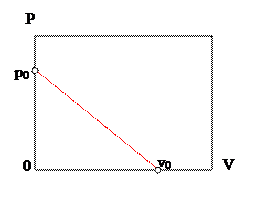
d Задача. Определите величину теплоемкости моля идеального одноатомного газа на прямой линии диаграммы P – V.

Уравнение прямой линии в координатах P – V

.

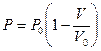Используемые уравнения (термическое и калорическое уравнения газа, первый закон термодинамики)

.

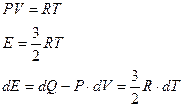Из последнего уравнения

.

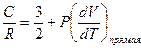Производную на прямой линии p₀ – v₀ определяем, используя уравнение прямой и термическое уравнение.

.

. .

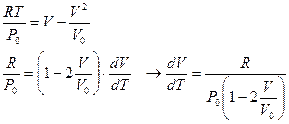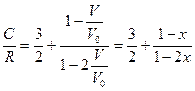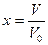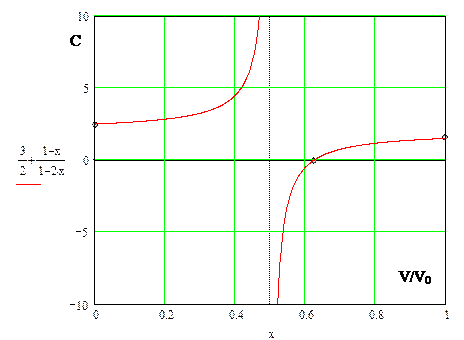График полученного результата показывает диапазон изменения теплоемкости вдоль прямой. В середине линии теплоемкость терпит разрыв. Граничные теплоемкости соответственно равны 5/2 и 3/2. В точке 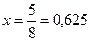теплоемкость равна 0.

d Задача. Получить уравнение политропического процесса. Политропическим процессом называется процесс при постоянной теплоемкости.

Будем использовать

.

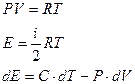Используя первые два уравнения, преобразуем дифференциальное уравнение первого закона термодинамики

.

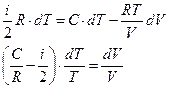Обозначим 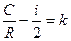. Дифференциальное уравнение политропы переписывается

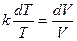. Интегрирование приводит к уравнению

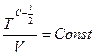. (10)
Здесь и далее теплоемкость выражена в единицах R.

• Изохорный процесс. Очевидно, что в этом случае .
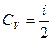• Изобарный процесс. В формуле (10) перейдем к давлению

.

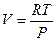
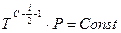Очевидно, что давление будет постоянным при условии 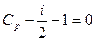. Отсюда

.

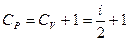• Адиабатный процесс. C = 0. Подстановка в (10) определяет уравнение адиабаты

.

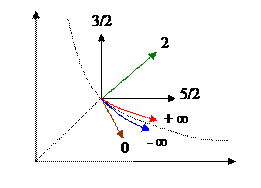
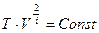• Изотермический процесс. Преобразуем формулу (10) к виду .

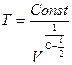Температура будет константой при условии .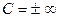

• Процесс с линейной зависимостью давления от объема. В формуле (10) избавляемся от температуры

.

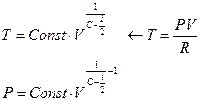Для линейной зависимости давления от объема необходимо выполнения условия

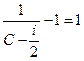. Отсюда получаем .

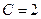Рисунок иллюстрирует спектр политропных процессов с различными теплоемкостями. Процессы идущие вблизи изотермы имеют бесконечные теплоемкости.

III. 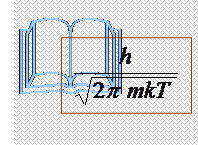Статистическая термодинамика.