2018-03-09
237
Часто на практике бывает достаточным иметь сведения только об общих закономерностях изменения кинематических параметров механизма за цикл, не предъявляя высоких требований к точности результатов. Тогда применяют метод кинематических диаграмм.
Н рис.2.8 а приведена кинематическая схема кривошипно-шатунного механизма. Известны 
- масштаб длин; 
- частота вращения кривошипа; 
- перемещения ползуна в зависимости от положения кривошипа.
На рис.2.8б. приводится порядок построения диаграммы перемещения S = f(
). По оси абсцисс отложен отрезок 0-11, длиной 
, соответствующий одному кинематическому циклу, т.е.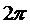 
(или времени одного оборота кривошипа - T), тогда:
, 
, 
Отрезок 0…11 разбит на столько частей, сколько положений кривошипа изображено на схеме механизма.
При этом точки 1,2,3 и т.д. на оси ординат соответствуют моментам времени, когда механизм занимает положения соответственно 1,2,3 и т.д. Из этих точек на вертикалях отложены перемещения: S(1) = (1-1s), S(2) = (2-2s) …. Соединение 0, 1s 2s, 3s … получена диаграмма S = f1() или S = f1(
), при этом 
- масштаб перемещения. Иногда есть необходимость увеличивать (уменьшать) Si в k раз, т.е. (i-iS)=kSi, тогда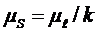 
.
Дифференцированием этого графика можно получить два остальных, так как между перемещением, скоростью и ускорением точки есть зависимость
и 
.
Рис.2.8. К исследованию механизма методом диаграмм
При графическом дифференцировании удобно применять метод хорд. Суть метода заключается в допущении, что секущая, соединяющая две соседние точки is - (i + 1)s участка дифференцируемой кривой, параллельна касательной, проведенной к средней его части. На рис.2.8. в показано получение точки 
.
1. Соединив точки 4s и 5s получена секущая линия 5 (рис.2.8.б)
2. Из точки (рис.2.8. в) p - полюса, находящейся на расстоянии HV мм от начала координат графика 
= f2(
), проведена 5’ параллельно линии 5 до пересечения с осью
3. Через эту точку проведена горизонталь 5г.
4. Через середину 4 и 5 на оси абсцисс проведена вертикаль 5в.
5. В пересечении линий 5г и 5в получена точка 5V.
В такой последовательности найдены точки 
, соединив которые плавной кривой получен график = f2()
Скорость ползуна точки В
(2.42)
где 
и 
- приращения по осям координат.
Отношение 
где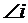 
- угол наклона касательной в точке 
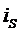. Тогда выражение 2.42 примет вид:
(2.43)
Из диаграммы:
(2.44)
где 
- масштаб скорости из диаграммы, 
- ордината в i -ом положении.
Из треугольника (слева от начала координат 0 с вершиной p и прямым углом в точке 0.
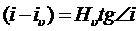
С учетом этого и приняв правые части 2.43 и 2.44 получим:
(2.45)
Таким образом, масштаб диаграммы зависит не только от масштабов дифференцируемой кривой, но и в большей степени от полюсного расстояния 
.
Дифференцированием = f2() можно получить график ускорения aB, при этом
,
где 
- полюсное расстояние на графике 
= f().
