Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на AT равен единичной матрице:
A*AT=AT*A=E;
или, что эквивалентно, её обратная матрица равна транспонированной матрице:
AT=A-1;
Столбцы и строки ортогональной матрицы образуют системы ортонормированных векторов, то есть:

и
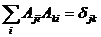

Где i 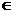 {1,…,n}, n — порядок матрицы, а
{1,…,n}, n — порядок матрицы, а  — символ Кронекера.
— символ Кронекера.
Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.
Определитель ортогональной матрицы равен, что следует из свойств определителей:
1=det(I)=det(ATA)=det(AT)det(A)=det(A)det(A)=det(A)2=1;
Множество ортогональных матриц порядка n над полем k образует группу по умножению, так называемую ортогональную группу которая обозначается On(k) или O(n,k= 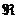 ) (если опускается, то предполагается).
) (если опускается, то предполагается).
Ортогональные матрицы соответствуют линейным операторам, переводящим ортонормированный базис линейного пространства в ортонормированный.
Теорема: матрица перехода от одного ортонормированного базиса к другому является ортогональной.
Доказательство: положим имеем два вектора

Запишем матрицы – столбцы координат этих векторов:
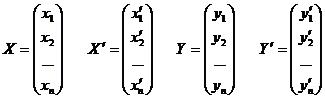
Скалярное произведение этих двух векторов:
 , или, в матричной записи:
, или, в матричной записи:
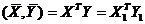 (*)
(*)
Если матрица перехода от одного базиса  к другому
к другому  есть S, то:
есть S, то:
X = S X1; Y = S Y1
Подставим в (*):

Отсюда ST×S = E или ST = S-1. Т.е. матрица S – ортогональная.
К примеру, матрица, осуществляющая поворот осей координат в одной из предыдущих лекций – это матрица перехода от одного ортонормированного базиса к другому. Она является ортогональной.
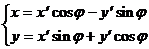
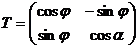
detT = 1, T-1 = T` = 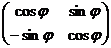
Ортогональные операторы
Линейный оператор  называется ортогональным, если
называется ортогональным, если

Для того чтобы оператор  был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.
был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.
Ортогональные операторы и только они сохраняют длину вектора, т. е.

 2018-02-13
2018-02-13 1604
1604
