Получим формулу для вычисления скалярного произведения по координатам сомножителей в ортонормированном базисе.
Е сли векторы в ортонормированном базисе заданы своими координатами  ,
,  , то скалярное произведение равно:
, то скалярное произведение равно:
|
|
Длина вектора a (  ) заданного координатами в ортонормированном базисе
) заданного координатами в ортонормированном базисе 
 ,
,  , вычисляется по формуле
, вычисляется по формуле
|
Координаты вектора в ортонормированном базисе: Любой вектор Аналогично плоскому случаю, помимо записи Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры: Базисные векторы записываются следующим образом: |
Метод ортогонализации Шмидта
Для справки:
Множество векторов называется ортогональной системой векторов (или системой попарно ортогональных векторов), если любые два ее вектора ортогональны (относительно данного скалярного произведения).
Всякая упорядоченная ортогональная система из n ненулевых векторов n-мерного евклидова векторного пространства образует его базис. Такой базис называется ортогональным.
Базис евклидово векторного пространства < V, g > называется ортонормированным, если все его векторы - попарно ортогональные орты (относительно скалярного произведения g).
Ответ:
a1…an – произвольный базис.
Положим вектор:  ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 |
 – ортогональный базис
– ортогональный базис
 - ортонормированный базис
- ортонормированный базис
 ;
;  ;
;  ;
;
Теорема:  - евклидово пространство, dim
- евклидово пространство, dim  =n
=n  в
в  существует ортонормированный базис.
существует ортонормированный базис.
Или так
Теорема: В любом ненулевом конечномерном евклидовом векторном пространстве существует ортонормированный базис.
 2018-02-13
2018-02-13 5648
5648



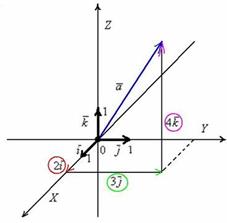
 трехмерного пространства можно единственным способом разложить по ортонормированному базису
трехмерного пространства можно единственным способом разложить по ортонормированному базису  :
:  , где
, где  – координаты вектора
– координаты вектора  (числа) в данном базисе.
(числа) в данном базисе.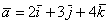 широко используются версии со скобками:
широко используются версии со скобками:  либо
либо  .
. (дотошно
(дотошно  ) – запишем
) – запишем  ;
; (дотошно
(дотошно  ) – запишем
) – запишем  ;
; (дотошно
(дотошно  ) – запишем
) – запишем  .
.