Квадратичной формой n переменных x1…xn называется однородный многочлен второй степени относительно этих переменных:
Ф(х1,..хn)=a11*x12+a12*x1*x2+…+a1n*x1*xn+a21*x2*x1+a22*x22+…+ann*xn2
В Матричном виде: Ф(х1,..хn)=ХТАХ
Где Х – столбец переменных х1…xn
А – (аij)n*n – матрица квадратичной формы Ф, симметричная
Квадратичную форму следует рассматривать как функцию, ставящую в соответствие каждому элементу х евклидова пространства Еn некоторое вещественное число Ф(x)6.
Приведение квадратичной формы к каноническому виду:
Пусть А – матрица квадратичной формы в старом ортонормированном базисе E. Мы должны подобрать такую смену базиса, чтобы в новом E’матрица квадратичной формы стала диагональной, то есть нужно подобрать невырожденную матрицу S=TE’->E, чтобы:
STAS=D= 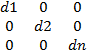
Рассмотрим линейный оператор (фи) такой, что [фи]E=А. Т.к. матрица А симметричная, то оператор фи самосопряженный. Значит для него существует ортонормированный базис из собственных векторов фи, который мы обозначаем за E’.
S-1AS= 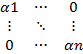
Алгоритм:
1)Записать матрицу А данной квадратичной формы Ф.
2)Найти собственные числа соответствующего самосопряженного оператора фи, то есть решить характеристическое уравнение |A- 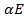 |=0. Пусть
|=0. Пусть  - собственные числа. Тогда канонический вид: Ф(x1’,…xn’)=
- собственные числа. Тогда канонический вид: Ф(x1’,…xn’)= 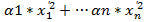
3)Найти собственные векторы оператора фи. Пусть это векторы a1 a2 … an. Если все корни характеристического уравнения простые, то эти векторы образуют ортогональный базис.Если есть кратные корни, то для собственных векторов соответствующих одному собственному значению, потребуется провести процесс ортогонализации.
4)из полученного ортогонального базиса сделать ортонормированный: ei= 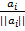 - искомый канонический базис.
- искомый канонический базис.
 2018-02-13
2018-02-13 884
884








