2018-03-09
122
Если разложение в ряд по степеням х в интервале сходимости (– R, R) включает в себя отрезок [ a, b ], то для вычисления данного интеграла можно воспользоваться свойством почленного интегрирования этогоряда. Ошибку вычислений определяют так же, как и при вычислении значений функции.
Пример 37. Вычислить интегралSi(x)= 
(интегральный синус).
• Имеем: sin t = t – 
+ 
– 
+ …, –∞ < t <∞.
Далее, 
=1 –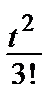 
+ 
– 
+ ….
Следовательно, Si(x)= = 
= x – 
+ 
– 
+ …, –∞ < x <∞.
Пример 38. Вычислить интеграл 
с точностью до ε = 0,001.
• Имеем: 
= 1 – 
+ 
– 
+ …, –∞ < x <∞.
Интегрируя обе части этого равенства на отрезке [0, 1/4], получим
= 
= 
=
= 
– 
+ 
– 
+ …, –∞ < x <∞, – ряд лейбницевского типа.
Т.к. ≈ 0,0052 > 0,001, а ≈ 0,0001 < 0,001, то с точностью до 0,001 имеем
≈ – 
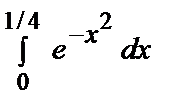= 0,245.
