Приближенное интегрирование дифференциальных уравнений

  Если интегрирование дифференциального уравнения не сводится к квадратурам, то для приближенного интегрирования можно воспользоваться рядом Тейлора.

  Пусть требуется найти частное решение у (x) уравнения

y′ = f (x, y),                                                           (1)

которое удовлетворяет начальным условиям у (x ₀) = у ₀. 

  Предположим, что искомое решение уравнения (1) в окрестности точки x ₀, в которой заданы начальные условия, можно разложить в ряд

у (x) = у (x ₀) + 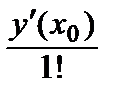(х – х ₀) + (х – х ₀)² + … + (х – х ₀) ⁿ + ….      (2)

  Нам надо найти у (x ₀), у′ (x ₀), у′′ (x ₀), …. Значение у (x ₀) = у ₀ задано начальными условиями. Чтобы найти у′ (x ₀) = у′ ₀ в уравнении (1) необходимо положить х = x ₀, у = у ₀. Производную 

у′′ (x ₀) = у′′ ₀   находим дифференцированием уравнения (1) по х:

у′′ = f ₁(x, y, у′),                                                              (3)

положив в этом равенстве х = x ₀, у = у ₀, у′ = у′ ₀. 

  Продифференцировав уравнение (3) и положив х = x ₀, у = у ₀, у′ = у′ ₀, у′′ = у′′ ₀, получим 

у′′′ (x ₀) = у′′′ ₀  и т.д. Процесс или обрывается на некотором коэффициенте, или заканчивается нахождением общего закона построения коэффициентов.

Замечание. По формуле (2) можно находить приближенное решение уравнения любого порядка

y ^{( n )} = f (x, y, y′, …, y ^{( n – 1)}) с начальными условиями у (x ₀) = у ₀, у′ (x ₀) = у′ ₀ , …, у ^{( n – 1)} (x ₀) = у ₀^{( n – 1)}.   

Пример 39. Найти три первых (отличных от нуля) члена разложения в ряд решения уравнения

y′′ = xy′ + y, y (0) = 0, y′ (0) = 1.

• Ищем решениеу (х) в виде ряда Маклорена: у (х) = у (0) + х + х ² + … + хⁿ + ….

Туту (0) = 0, y′ (0) = 1, y′′ (0) = 0 ∙ 1 + 0 = 0.

   Последовательно дифференцируя данное уравнение, получим

y′′′ = y′ + xy′′ + y′ = 2 y′ + xy′′,y′′′ (0) = 2;

y ^IV= 2 y′′ + y′′ + xy′′′ = 3 y′′ + xy′′′, y ^IV(0) = 0;

y ^V= 3 y′′′ + y′′′ + xy ^IV = 4 y′′′ + x y ^IV, y ^V(0) = 8.

Подставляя найденные производные в ряд Маклорена, получим искомое решение

у (х) ≈ х + х ³ + х ⁵= х + + .

Пример 40. Найти три первых (отличных от нуля) члена разложения в ряд решения уравнения

y′ = x ² + y ³, y (1) = –1.

• Ищем решениеу (х) в виде ряда Тейлора: у (х) = у (1) + (х – 1) + (х – 1)² + … + (х – 1) ⁿ + ….

Имеем у (1) = –1, y′ (1) = 1² + (–1)³ = 0;   y′′ = 2 x + 3 y ² y′, y′′ (1) = 2; y′′′ = 2 + 6 y (y′)² + 3 y ² y′′, y′′′ (1) = 8.

Т.о.,        у (х) ≈ –1 + (х – 1)² + (х – 1)³= –1 + (х – 1)² + 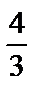(х – 1)³.

 

 

 

РЯДЫ ФУРЬЕ

Определение

Пусть функция f (x) интегрируемая и периодическая с периодом 2 π. Коэффициентами Фурье функции f (x) называются числа а ₀, а ₁, а ₂, …, а_n, …, b ₀, b ₁, b ₂, …, b_n, …, которые находятся по формулам

а ₀ = 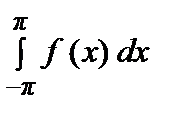, а_n = , b_n = (n = 1, 2, …). (1)

Тригонометрическим рядом Фурье функции f (x) называется ряд

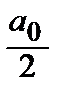+ .                                                  (2)