Пусть f (x) – периодическая с периодом 2 l функция, удовлетворяющая условиям теоремы Дирихле на интервале (– l, l). Тогда ее разложение в ряд Фурье имеет следующий вид:
f (x) = 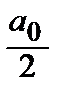 +
+ 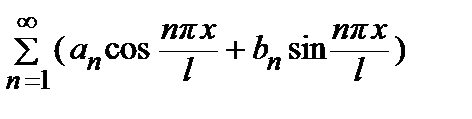 ,
,
где а 0 = 
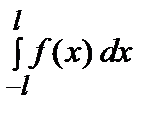 , аn =
, аn = 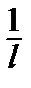
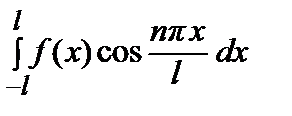 , bn =
, bn = 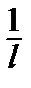
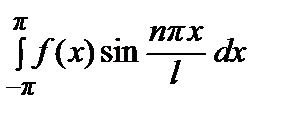 (n = 1, 2, …).
(n = 1, 2, …).
Ряд Фурье четной функции f (x) содержит только свободный член и косинусы
f (x) = 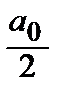 +
+ 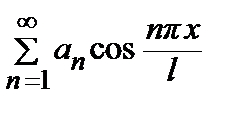 ,
,
где а 0 = 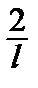
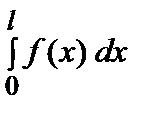 , аn =
, аn = 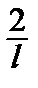
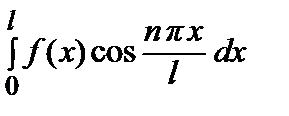 (n = 1, 2, …).
(n = 1, 2, …).
Нечетная функция f (x) разлагается в ряд Фурье по синусам f (x) = 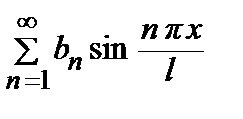 ,
,
где bn = 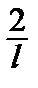
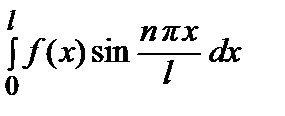 (n = 1, 2, …).
(n = 1, 2, …).

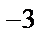
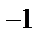
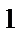
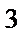
Пример 45. Разложить в ряд Фурье функцию, представленную на рисунке.
• Имеем f (x) = х 2, –1 ≤ х ≤ 1, f (x + 2) = f (x), х 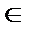 (–∞, +∞).
(–∞, +∞).
Эта функция непрерывна на всей числовой оси, четная и имеет период 2 l = 2,
Поэтому а 0= 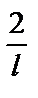
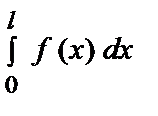 = 2
= 2 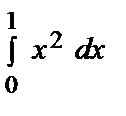 =
= 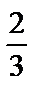 . an =
. an = 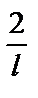
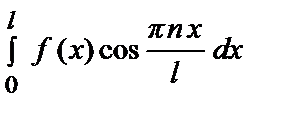 = 2
= 2 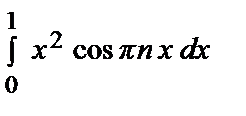 =
=
= 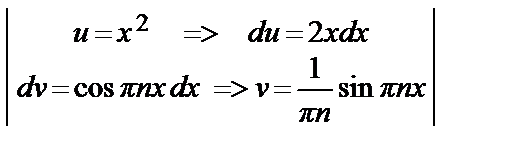 = 2
= 2 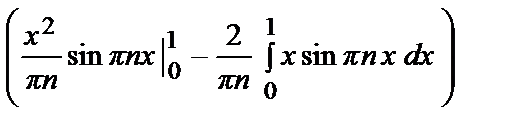 = –
= – 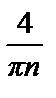
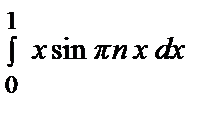 =
=
= 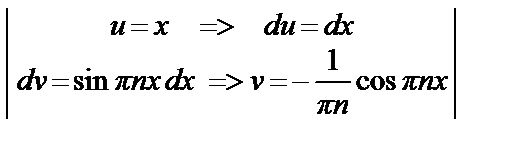 = –
= – 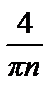
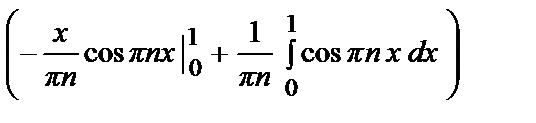 = –
= – 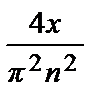
 =
= 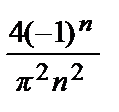 .
.
bn = 0.
f (x) = 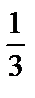 +
+ 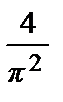
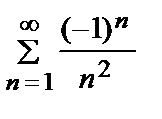 cosπ nx =
cosπ nx = 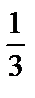 +
+ 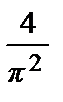 (–
(–  +
+ 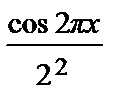 –
– 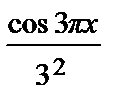 +
+ 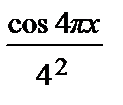 – …)(–∞ ≤ х ≤ ∞).
– …)(–∞ ≤ х ≤ ∞).
 2018-03-09
2018-03-09 186
186








