Ряд Фурье интегрируемой функции f (x) может либо расходиться, либо сходиться, причем как к функции
f (x), так и к функции, отличной от нее. Условия сходимости ряда Фурье были установлены немецким математиком Дирихле.
Теорема Дирихле. Если функция f (x) непрерывна или имеет конечное число точек разрыва на отрезке
[- π, π ] и при этом монотонна или имеет конечное число экстремумов на [- π, π ], то ряд Фурье функции
f (x) сходится для любых х из [- π, π ] и его сумма равна:
1) f (x) для всех точек непрерывности х из интервала (- π, π);
2) 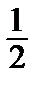 (f (x 0 – 0) + f (x 0 + 0)) для всех точек разрыва x 0;
(f (x 0 – 0) + f (x 0 + 0)) для всех точек разрыва x 0;
3) 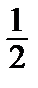 (f (– π + 0) + f (π – 0)) при х = – π и х = π.
(f (– π + 0) + f (π – 0)) при х = – π и х = π.
Пример 41. Разложить в ряд Фурье 2 π - периодическую функцию f (x) = π + x, x 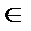 (- π, π ] (см. рис.).
(- π, π ] (см. рис.).
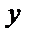
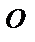
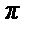
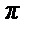
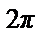
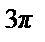
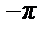 • Заданные функции кусочно-монотонны на промежутке (- π, π ], поэтому ее
• Заданные функции кусочно-монотонны на промежутке (- π, π ], поэтому ее
можно представить рядом Фурье. Т.о.,задача сводитсяк нахождению
коэффициентов Фурье.
 a 0=
a 0= 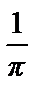
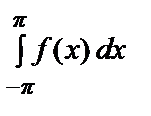 =
= 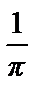
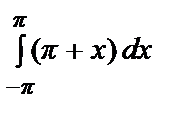 =
= 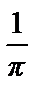
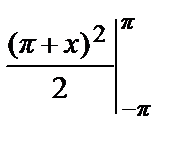 = 2 π.
= 2 π.
an = 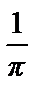
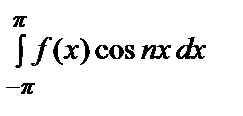 =
= 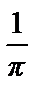
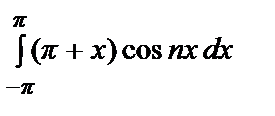 =
= 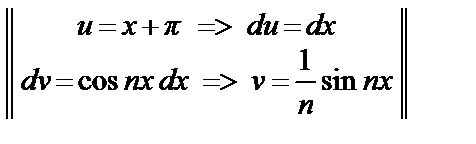 =
=
= 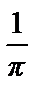
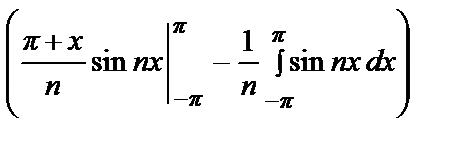 = 0.
= 0.
bn = 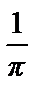
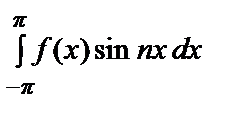 =
= 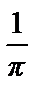
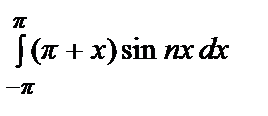 =
= 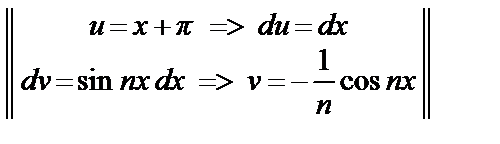 =
=
= 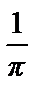
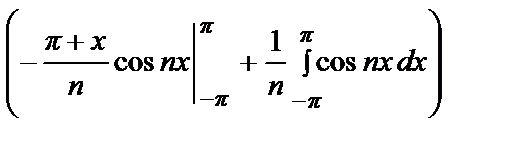 = –
= – 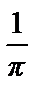
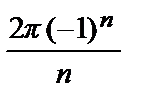 =
= 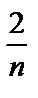 (–1) n + 1.
(–1) n + 1.
Подставив найденные коэффициенты в ряд (2), получимf (x) = π + 2 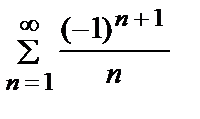 sin nx.
sin nx.
Это равенство справедливо для всех точек непрерывности заданной функции, т.е. прих ≠ ±(2 n – 1) π, n 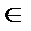 N.
N.
В точках ±(2 n – 1) π сумма ряда Фурье равняется π (полусумме односторонних границ в этих точках).
Пример 42. Разложить в ряд Фурье 2 π - периодическую функцию f (x) = 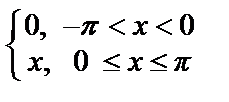 (см. рис.).
(см. рис.).
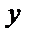

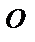
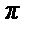
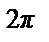
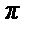
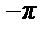
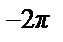 • a 0=
• a 0= 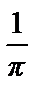
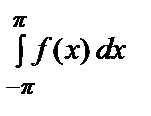 =
= 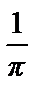
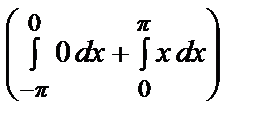 =
= 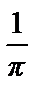
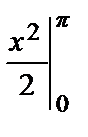 =
= 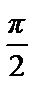 .
.
an = 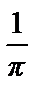
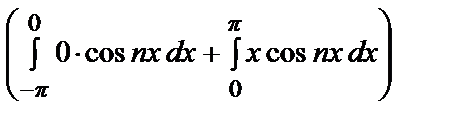 =
= 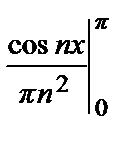 =
= 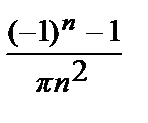 .
.
bn = 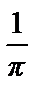
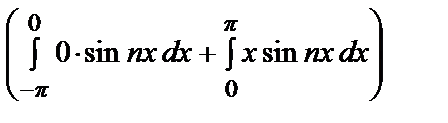 = –
= – 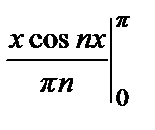 =
= 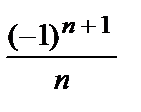 .
.
Т.о., ряд Фурье заданной функции имеет вид f (x) = 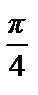 +
+ 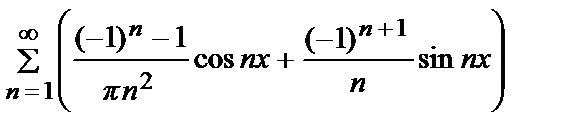 =
=
= 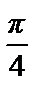 –
– 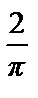
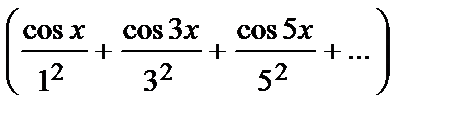 +
+ 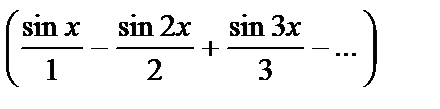 .
.
Найденный ряд сходится к функции f (x) при всех х ≠ ±(2 n – 1) π, n 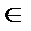 N. В точках х = ±(2 n – 1) π сумма ряда
N. В точках х = ±(2 n – 1) π сумма ряда
Фурье равняется 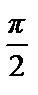 (полусумме односторонних границ в этих точках).
(полусумме односторонних границ в этих точках).
Ряд Фурье для четных и нечетных функций
Пусть f (x) – четная функция (f (– x) = f (x),  х
х 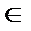 [- π, π ]). Тогда bn = 0 (n = 1, 2, …), и, следовательно, четная функция разлагается в ряд Фурье по косинусам:
[- π, π ]). Тогда bn = 0 (n = 1, 2, …), и, следовательно, четная функция разлагается в ряд Фурье по косинусам:
f (x)= 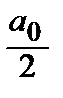 +
+ 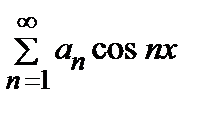 ,
,
где а 0 = 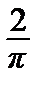
 , аn =
, аn = 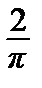
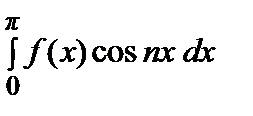 , (n = 1, 2, …). (3)
, (n = 1, 2, …). (3)
Аналогично, нечетная функция f (x)(f (– x) = – f (x),  х
х 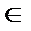 [- π, π ]) разлагается в ряд Фурье по синусам:
[- π, π ]) разлагается в ряд Фурье по синусам:
f (x)= 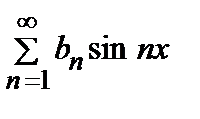 ,
,
где bn = 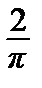
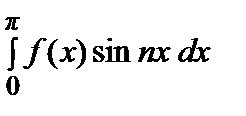 , (n = 1, 2, …).(4)
, (n = 1, 2, …).(4)
Пример 43. Разложить в ряд Фурье 2 π - периодическую функцию f (x) = |x |, x 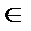 [- π, π ] (см. рис.).
[- π, π ] (см. рис.).
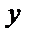

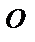
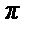
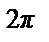
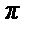
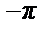
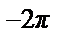 • Т.к. функцияf (x) четная, то
• Т.к. функцияf (x) четная, то
a 0= 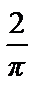
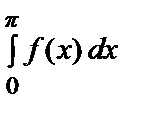 =
= 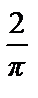
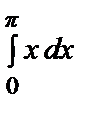 =
= 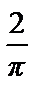
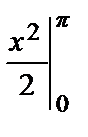 = π.
= π.
an = 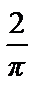
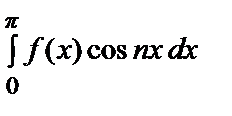 =
= 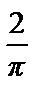
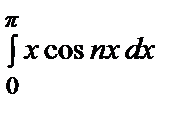 =
= 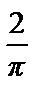
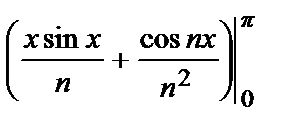 =
= 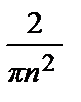 ((–1) n – 1); bn = 0.
((–1) n – 1); bn = 0.
f (x) = 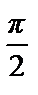 +
+ 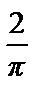
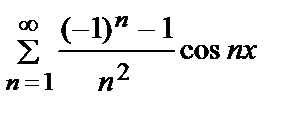 =
= 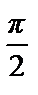 –
– 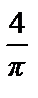
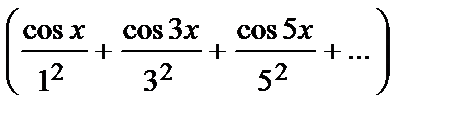 .
.
Пример44. Разложить в ряд Фурье 2 π - периодическую функцию f (x) = 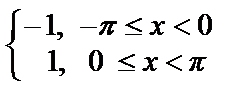 (см. рис.).
(см. рис.).

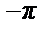 • Т.к. функция f (x) нечетная, тоa 0=0; аn =0.
• Т.к. функция f (x) нечетная, тоa 0=0; аn =0.
bn = 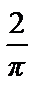
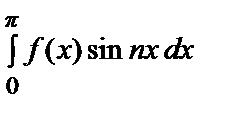 =
= 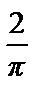
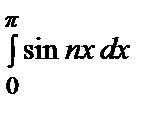 = –
= – 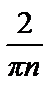
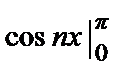 = –
= – 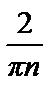 ((–1) n – 1).
((–1) n – 1).
f (x) = 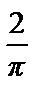
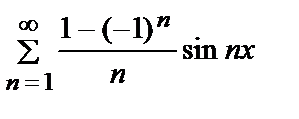 =
= 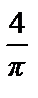
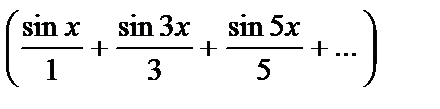 .
.
Это равенство справедливо во всех точках x 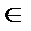 (- ∞, + ∞), кроме точек разрыва. В точках разрыва
(- ∞, + ∞), кроме точек разрыва. В точках разрыва
х =0, ± π, ±2 π, ±3 π, … сумма найденного ряда равна нулю.
 2018-03-09
2018-03-09 135
135








