f (x) = 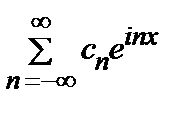 , cn =
, cn = 
 , n = 0, ±1, ±2, …
, n = 0, ±1, ±2, …
При получении комплексных коэффициентов Фурье используются формулы Эйлера:
einx = cos nx + i sin nx, e–inx = cos nx – i sin nx,
из которых получаем:cos nx =  , sin nx =
, sin nx =  = i
= i  .
.
| - 2 π |
| -π |
| 2 π |
| π |
| O |
| x |
f (x) =  .
.
• Имеем:
cn = 
 =
= 
 =
= 
 =
=  =
=  =
=  =
=
= i 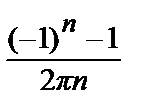 =
= 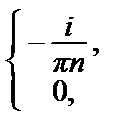
 или, короче, c 2 n –1 = –
или, короче, c 2 n –1 = –  , c 2 n = 0.
, c 2 n = 0.
Подставляя значенияcnв ряд Фурье, получимf (x) =  =
= 
 , – π < x < 0, 0 < x < π.
, – π < x < 0, 0 < x < π.
Таблица разложения некоторых функций в ряд Фурье
1. y = x, – π < x < π: y = 2  .
.
2. y = | x |, – π < x < π: y =  –
– 
 .
.
3. y = x, 0 ≤ x ≤ 2 π: y = π – 2  .
.
4. y = 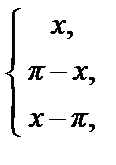
 : y =
: y = 
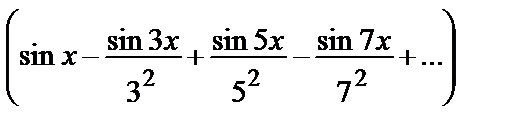 .
.
5. y = 
 a > 0: y =
a > 0: y = 
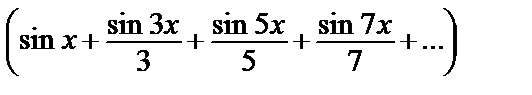 .
.
6. y = 
 : y =
: y =  –2·
–2· 
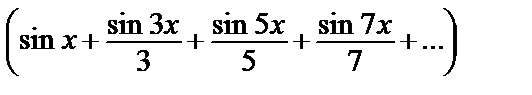 .
.
7. y = 
 a >0, 0< α <
a >0, 0< α <  : y =
: y = 
 .
.
8. y = x 2, – π < x < π: y =  – 4·
– 4·  .
.
9. y = 
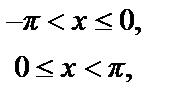 : y =2 π ·
: y =2 π ·  –
–  ·
·  .
.
10.  : y =
: y =  –
–  .
.
11.  : y =
: y = 
 .
.
12. y = ax 2 + bx + c, – π < x < π: y =  + c + 4 a
+ c + 4 a  – 2 b
– 2 b  .
.
13. y = | sin x|, – π ≤ x ≤ π: y =  –
–  ·
·  .
.
14.  : y =
: y = 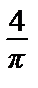
 .
.
15. y = 
 : y =
: y =  +
+  sin x –
sin x –  ·
·  .
.
16.  : y =
: y = 
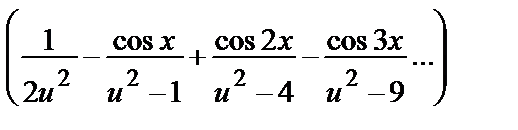 .
.
17. 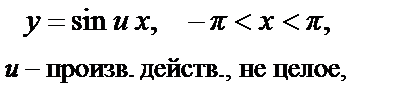 : y =
: y = 
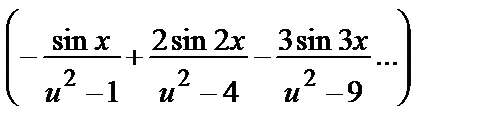 .
.
18. y = x cos x, – π < x < π: y =  .
.
19. y = x sin x, – π ≤ x ≤ π: y = 1  –2·
–2·  .
.
20. y = eax, – π < x < π: y = 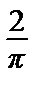 sh aπ
sh aπ  .
.
Разложение различных периодических функций нередко можно получить путем изменения масштаба разложения табличных функций как по оси Ох, так и по оси Оу.
Пример 49. Найти разложение вряд Фурье периодической функции y = x +1, 0 < x < 2Tcпериодом 2T.
• Сделаем замену переменных Y=  , X=
, X=  , при которой наша функция преобразуется к
, при которой наша функция преобразуется к
виду Y= Х, – π <Х< π, с периодом 2 π.Эта функция имеет разложение в ряд Фурье (см. п. 1 таблицы)
Y = 2 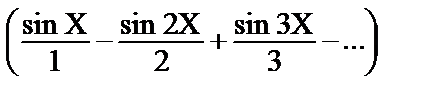 .
.
Возвращаясь к старым координатам, получим:
 = 2
= 2  .
.
Т.о., y =(T+1) – 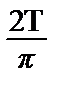

Пример 50. Найти разложение в ряд Фурье периодической функции y = x, 0 < x ≤ 2 π cпериодом 2 π.
•Y= y – π, X= x – π => при которой наша функция преобразуется к виду Y=Х, – π <Х< π, с периодом 2 π.Эта функция разлагается в ряд Фурье (см. п. 1 таблицы)Y = 2 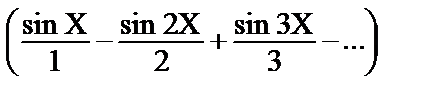 .
.
Возвращаясь к старым координатам, получим: y – π = 2  .
.
Т.о., y = π – 2  .
.
 2018-03-09
2018-03-09 154
154







