2018-03-09
155
Четное и нечетное продолжение функции
Пусть f (x) – непериодическая функция, заданная на всей числовой оси (–∞ ≤ х ≤ ∞). Такая функция не может быть разложена в ряд Фурье, т.к. сумма ряда Фурье есть функция периодическая и, следовательно, не может быть равна f (x) для всех х.
Однако, непериодическая функцияf (x) может быть 
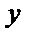
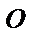
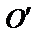
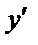
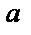
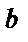
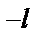
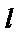представлена
в виде ряда Фурье на любом конечном промежутке [ a; b ],
на котором она удовлетворяет условиям Дирихле. Для этого можно
поместить начало координат в середину отрезка [ a; b ] и построить Рис.1.
функцию f 1(x) периода T = 2 l = | b – a | такую, что f 1(x) = f (x)
при –l ≤ x ≤ l (см. рис.1).
Разлагаем функцию f 1(x) в ряд Фурье. Сумма этого ряда
во всех точках отрезка [ a; b ] (кроме точек разрыва) совпадает с заданной функцией f (x). Вне этого промежутка сумма ряда и f (x) являются совершенно различными функциями.
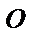
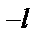
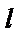
На практике поступают несколько иначе: начало координат переносится
в точку х = а отрезка [ a; b ]. Область определения функции f (x) будет
|
|
|
иметь вид [0; l ], где l = | b – a |. Такую функцию можно произвольным
образом доопределить на отрезке [ –l; 0], а затем осуществить ее
периодическое продолжение с периодом T = 2 l. Разложив в ряд Фурье Рис.2.
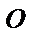
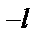
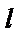
на отрезке [ –l; l ] 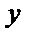полученную таким образом периодическую функцию f 1(x),
получим искомый ряд для функции f (x) при х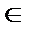 
[0; l ].
В частности, функциюf (x) можно доопределить на отрезке [ –l; 0]
четным образом (рис.2). В этом случае функцияf (x) разлагается в ряд
Фурье, который содержит только косинусы.
Если же функциюf (x) продолжитьна отрезке [ –l; 0] нечетным Рис.3.
образом (рис.3), то она разлагается в ряд, состоящий только из синусов.
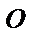
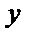
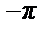
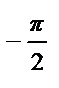
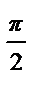
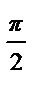
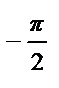
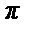Ряд косинусов и синусов для функции f (x), заданной на отрезке [0; l ], имеют одну и ту же сумму. Если х 0 – точка разрыва функции f (x), то сумма как одного, так и другого ряда равна одному и тому же числу: S (х 0) = 
.
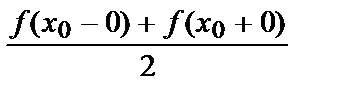Пример 46. Разложить в ряд Фурье по синусам на отрезке [0; π ] функцию,
f (x) =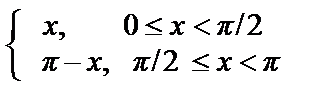 
.
• Продолжим функцию на отрезок [– π; 0] нечетным образом (см.рис.). Тогда
полученная функция нечетная и ее ряд Фурье содержит только синусы. Найдем
коэффициенты bn (n = 1, 2, …): bn =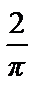 
= 
+ 
=
= 
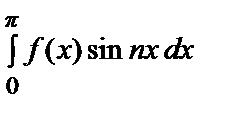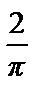
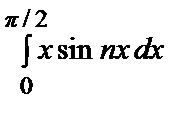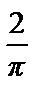
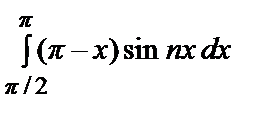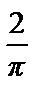
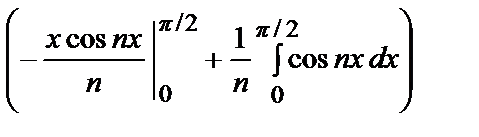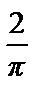+ ∙ π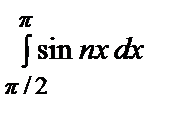 
– 
= 
+
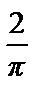
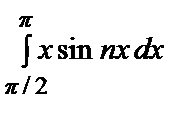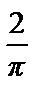
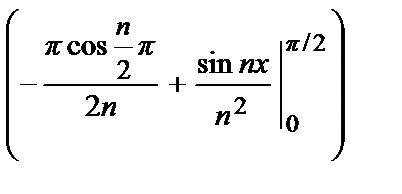+ 2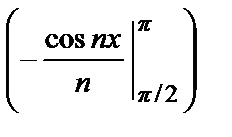 
– 
= – 
+ 
– 
+ 
+ 
–
– – 
= + = 
= 
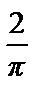
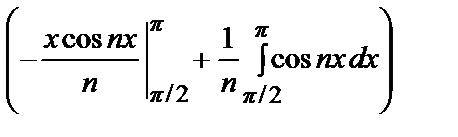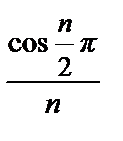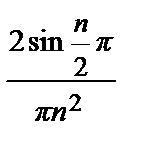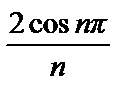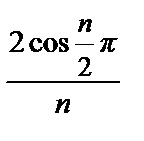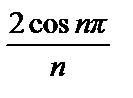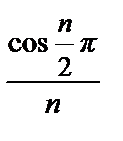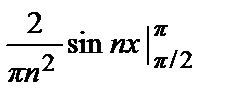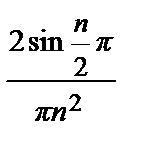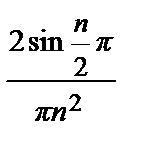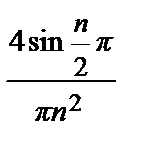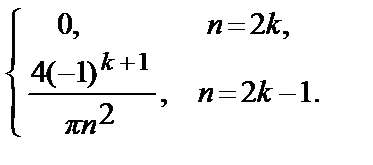
Т.о., f (x) =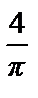 
.
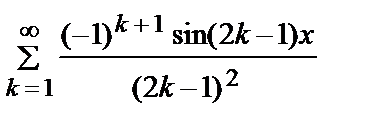При х =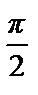 
имеем: 
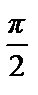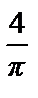= (1 +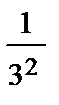 
+ 
+ … + 
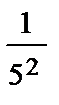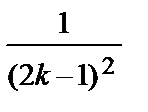+ …), откуда получаем, что сумма ряда
1 + 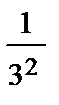+ + 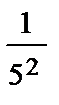… + + … 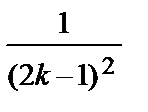равна 
.
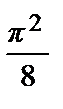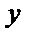
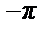
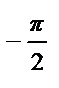
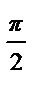
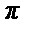
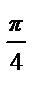
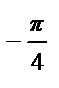Пример 47. Разложить в ряд Фурье по косинусам на отрезке [0; π ]
функцию f (x) =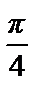 
– 
.
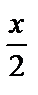• Продолжимданную функцию на отрезок [– π; 0] четным образом
(см.рис.). В результате получится четная функция, ряд Фурье которой состоит
|
|
|
только из косинусов. Вычислим коэффициенты аn (n = 0, 1, 2, …):
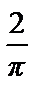
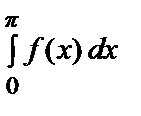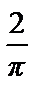
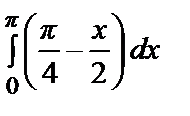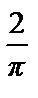
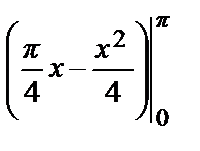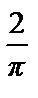
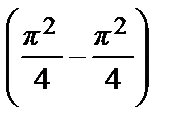a 0= 
= 
= 
= 
= 0.
an =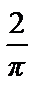 
= 
= 
– 
=
= 
– 
+ 
= 
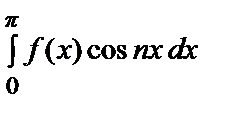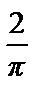
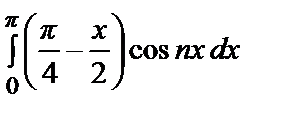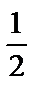
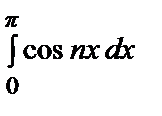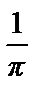
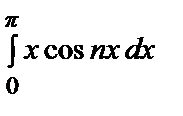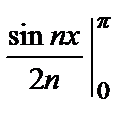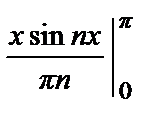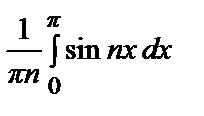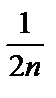(sin πn – sin 0) – 
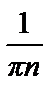(π sin πn – 0 ∙ sin 0) – 
=
= – 
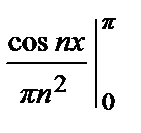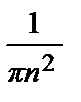(cos πn – cos 0) = – 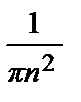(1 – (–1) n) =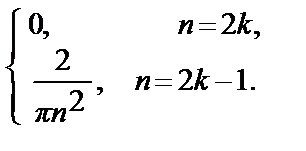 
Т.о., f (x) =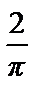 
.
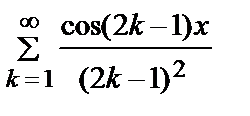Положим в этой формуле х = 0. Тогда: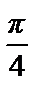 
= 
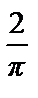
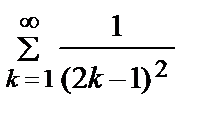. Откуда
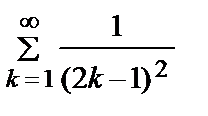= 1 + 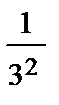+ + 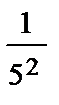… + + … 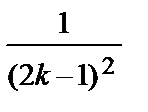= 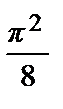(см. пример 46).
