Обчислення за допомогою степеневих рядів

Розглядатимемо такі функції  які є сумами своїх рядів Маклорена:

Беручи суму декількох перших членів цього ряду, отримуємо наближену формулу  при цьому залишок ряду   дає помилку, що виникає при заміні функції 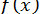многочленом 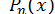. Оцінка залишку ряду дозволяє визначити потрібну для досягнення заданої точності кількість доданків, іншими словами, степінь многочлена .

Розглянемо, наприклад, обчислення показникової функції. Для  має місце розкладення

Позначаючи загальний член цього розкладення через  можемо записати .

Далі, ,  та , , . приблизно дає шуканий результат, кількість доданків визначається таким чином. Нехай спочатку . В цьому випадку для залишку ряду маємо:

оскільки

Тому 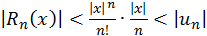 при ,  отже, процес додавання можна припинити, як тільки черговий член ряду (3) буде за модулем менше заданої похибки , тобто як тільки  (іноді кінець визначають попереднім вибором за формулою залишкового члена). При великих за модулем значеннях  ряд  збігається повільно, тому слід виділити цілу та дробову частину та записати . Перший множник  знаходиться перемножуванням  разів , якщо , якщо ж , то, обчисливши добуток (  повторюється множником  разів), знаходимо потім . Для обчислення другого множника 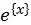 використовуємо розкладення , яке у випадку  збігається дуже швидко, оскільки

ПРИКЛАД 10. Знайти    з точністю до .

Враховуючи, що в цьому прикладі , , , і зберігаючи в проміжних обчисленнях два запасні десяткові знаки, отримуємо

.

Отже,  точністю до .

Для обчислення значення показникової функції                можна використати формулу .

ПРИКЛАД 11. Обчислити  точністю до .

Для обчислення значень  використовуємо степеневе розкладення

Цей ряд при великих  збігається повільно, але, враховуючи періодичність і формули приведення тригонометричних функцій, не важко бачити, що досить уміти обчислювати  (та ) для .

Формули для обчислення , як і для , можуть бути записані у вигляді

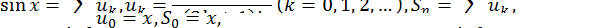
Оскільки при ряд  знакозмінний, загальний член якого прямує до нуля, монотонно спадаючи за модулем, то для залишка  справедлива оцінка . Отже, процес обчислення  можна припинити, як тільки черговий член ряду за модулем буде менше заданої похибки .

Враховуючи ці міркування, знаходимо , чи, виражаючи аргумент в радіанах,

.

Отже, .

Зауваження про чебишевські наближення. Як відомо, ряди Тейлора швидко збігаються, взагалі кажучи, тільки при малих значеннях . За допомогою многочленів Чебишева можна побудувати многочленне наближення, яке давало б задану точність для усіх точок даного відрізку.