Для студентов специальности 290700 и 290300

ТОЛЬЯТТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Водоснабжение и вентиляция»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ ПО ДИСЦИПЛИНЕ «ГИДРАВЛИКА»

для студентов специальности 290700 и 290300.

Тольятти 2004

УДК 532.5 (533.6)

Методические указания к лабораторным работам по дисциплине «Гидравлика» для студентовиальности 290700 и 290300. /Сост. Калинин А.В. – Тольятти: ТГУ, 2004.

Изложены цели, задачи и программа лабораторных работ, даны указания по подготовке к работам и их выполнению.

Для студентов специальностей: 2907, 2903, очной и очно – заочной формы обучения.

Ил.17. Табл. 12. Библиогр.: 5 назв.

Составитель: Калинин А.В.

Научный редактор: Вдовин Ю.И.

Утверждено редакционно-издательской секцией методического совета института.

ОПИСАНИЕ

универсального гидравлического стенда ГС 3

Универсальный гидростенд предназначен для проведения лабораторных работ по дисциплине «Гидравлика». Гидростенд разработан на кафедре «Теплотехника и тепловые двигатели» Самарского аэродинамического университета.

Рис. 1 Схема гидростенда.

Основные элементы гидростенда:

-напорное и приёмное устройство;

-рабочий участок;

-насос;

-измерительные устройства.

На стойке 4 (см. схему гидростенда) установлен расходный бачок 2, выполненный из нержавеющей стали в виде сферы. Расходный бачок имеет выходной патрубок 3, к которому с помощью уплотнения крепится рабочий участок 15. Другой конец рабочего участка укрепляется в патрубке с помощью резиновой манжеты, надвигаемой на участок механизмом 17.

В напорную магистраль вода поступает от насоса 9 при открытии вентиля 8. Во время эксперимента питающий вентиль 6 и сливной 7 должны быть закрыты. Расход воды через рабочий участок регулируется вентилем 18 на выходе из рабочего участка и вентилем 8

Приёмное устройство представляет собой бак 22, соединённый со сливной магистралью 12. Над приемным баком на консоли 10 смонтирован мерный бачок 20 для измерения расхода воды. На консоли установлен лоток 11, используемый для сбора воды и слива её в мерный бачок 20. В днище мерного бачка имеется клапан 21, управляемый с помощью рычажного механизма 19.

Измерительные приборы представлены пьезометрическим щитом 13, на котором смонтировано семь стеклянных трубок. Избыточное давление в расходном баке измеряется образцовым манометром 1. При измерении расхода воды одновременно с закрытием клапана на пульте управления 5 включается электросекундомер. После заполнения водой определённого объема мерного бака (3 литра) происходит замыкание контакта включателя уровня с одновременной остановкой электросекундомера.

Гидростенд работает по замкнутой схеме с насосной подачей воды из расходного бака, слива её в приёмный бак и подачей под напором в расходный бак.

ЛАБОРАТОРНАЯ РАБОТА №1

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ ВИСКОЗИМЕТРОМ ЭНГЛЕРА

1. ЦЕЛЬ РАБОТЫ

Приобретение навыков экспериментального определения вязкости исследуемой жидкости при помощи вискозиметра Энглера.

2. ВЯЗКОСТЬ ЖИДКОСТИ

При движении реальной жидкости между ее отдельными слоями возникают внутренниесилы трения, величина которых зависят от вида жидкости и характера распределения скоростей между слоями.

Согласно гипотезе Ньютона, подтвержденной экспериментальными исследованиями, касательное напряжение трения в жидкости определяется зависимостью:

, (1.1)

где μ - коэффициент динамическойвязкости;

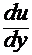- градиент скорости.

Коэффициент μ характеризует вязкость жидкости, т.е. свойство жидкости оказывать сопротивление относительному сдвигу частиц жидкости. Вязкость жидкостей зависит от температуры идавления.С повышением температуры вязкость капельных жидкостей уменьшается, а газов - увеличивается, что объясняетсяразличием их молекулярного строения. В капельных жидкостях вязкость вызывается силами молекулярного сцепления, которые уменьшаются с увеличением температуры. В газах вязкость обусловлена беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повышение температуры, что приводит к увеличению взаимодействия молекулгаза при ихстолкновении.

Для чистой пресной воды зависимость μ от температуры t определяется по формуле Пуазейля:

(1.2)

Для воздуха применяется формула Милликена:

(1.3)

Придавлениях, встречающихсяна практике (до 200 атм),вязкость капельных жидкостей мало зависит отдавления, и этим изменением обычно пренебрегают. Вязкость газовуменьшается с увеличением давления.

Динамическая вязкость измеряется в Па·с {СИ}:

1Па·с = 0,102 = 10 = 10 П (Пуаз)

Кроме динамической вязкости μ в гидравлике применяется кинематический коэффициент вязкости ν:

, (1.4)

где ρ – плотность жидкости.

Кинематическая вязкость измеряется в м²/с:

1 м²/с = 1·10⁴ см²/с = 1·10⁴ Ст (Стокс).

На практике вязкость жидкостей определяется вискозиметрами. Наиболее широкое распространение получил вискозиметр Энглера. При определении ν, см²/с можно пользоваться формулой Убеллоде:

, (1.5)

где ºЭ – градусы Энглера:

, (1.6)

здесь: τ₁– время истечения заданного объёма испытуемой

жидкости;

τ₂ – время истечения эталонной жидкости

(дистиллированная вода).

Градиент скорости в формуле (1.1) характеризует относительное изменение скорости между отдельными слоями потока.

Возьмём два слоя А и В (рис. 1.1), которые расположены на

Рис. 1.1. Распределение скоростей при течении жидкости в трубе.

расстоянии Δy один от другого. Слой В движется со скоростью U, а слой А со скоростью u+Δu. Величина Δu является абсолютным сдвигом слоя А

по слою В, а есть градиент скорости. Если слои будут находиться бесконечно близко друг к другу, то для двух соседних слоёв градиент скорости будет .

3. ПРОГРАММА РАБОТЫ.

1. Определить вязкость испытуемой жидкости при помощи вискозиметра Энглера.

2. Измерить ареометром плотность жидкости.

3. Установить динамическую вязкость испытуемой жидкости.

4. ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ.

Вискозиметр Энглера (рис. 1.2) состоит из металлического цилиндра 1, имеющего сферическое дно с отверстием. Отверстие закрывается стержнем 2. При исследовании зависимости изменения вязкости жидкости от температуры цилиндр помещается в водяную ванну 3 с регулируемым подогревом воды.

Рис. 1.2. Вискозиметр Энглера.

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Наливаем ≈ 250 см³ исследуемой жидкости в цилиндр 1 и устанавливаем мерный сосуд под отверстием.

2. Стержнем 2 открываем отверстие в цилиндре, одновременно включив секундомер.

3. Определяем время τ₁ истечения из цилиндра 200 см³ исследуемой жидкости при комнатной температуре. Опыт повторяем не менее 3 раз.

4. Тщательно вытираем цилиндр и в него выливаем при закрытом донном отверстии ≈250 см³ эталонной жидкости (дистиллированной воды).

5. Определяем время истечения τ₂ эталонной жидкости.

6. Для определения плотности исследуемую жидкость наливаем в высокий мерный стакан. В стакан опускаем ареометр и по ареометрической шкале определяем плотность жидкости.

7. Определяем среднее время истечения τ_1ср и τ_2ср

где n – количество измерений.

8. Вычисляем градусы Энглера

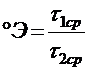9. Определяем коэффициент кинематической вязкости ν по формуле (1.5).

10. Находим динамический коэффициент вязкости μ по формуле (1.4).

11. Выполняем перевод полученных значений ν и μ из системы СГС в систему СИ. Результаты измерений и расчетов сводятся в таблицу 1.1.

6. КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. От чего зависит величина силы трения при движении жидкости?

2. Что называется вязкостью жидкости?

3. Что такое градиент скорости?

4. Какие коэффициенты вязкости Вы знаете, как они определяются?

5. Как изменяется вязкость жидкостей и газов с изменением температуры и давления?

6. Чем объясняется наличие вязкости в жидкостях и газах?

Таблица 1.1

№ опыта

жидкость

Время истечения τ, с

Среднее время τ _ср, с

Температура t, С

Плотность ρ

г/см³

Вязкость испытуемой жидкости

°Э

см² ^С

Стокс

санти- стокс

м² ^С

г с · см

Пуаз

Па · с

1. 2. 3.

ЛАБОРАТОРНАЯ РАБОТА №2.

ОПЫТНАЯ ДЕМОНСТРАЦИЯ ЗАКОНА ПАСКАЛЯ.

1. ЦЕЛЬ РАБОТЫ.

Экспериментальное исследование закона Паскаля с применением основного закона гидростатики в трубе переменного сечения.

2. ЗАКОН ПАСКАЛЯ. ПОНЯТИЕ О МАНОМЕТРИЧЕСКОМ, ВАКУУМЕТРИЧЕСКОМ, АБСОЛЮТНОМ ДАВЛЕНИИ.

Из основного уравнения гидростатики

(2.1)

следует, что всякое изменение внешнего давления на свободной поверхности жидкости, находящейся в равновесии, передается одинаково всем частицам жидкости по всем направлениям (закон Паскаля):

, (2.2)

где: z – геометрическая высота, определяемая расстоянием от плоскости сравнения до точки на свободной поверхности жидкости z₀ или до рассматриваемой точки в жидкости z₁:

p₀ и p₁ – давление на свободной поверхности и в рассматриваемой точке соответственно;

γ – удельный вес жидкости;

- пьезометрическая высота;

Δp – изменение давления.

Из уравнения (2.2) следует, что

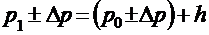, (2.3)

где h = (z₀- z₁)

Давления p₀ и p₁ в уравнении (1.3) являются абсолютными, т.к. отсчитываются по абсолютной шкале, имеющей начало отсчета, равное нулевому давлению (рис.1.1.).

Рис. 2.1. Шкала абсолютного, манометрического и

вакуумметрического давлений.

Превышение давления над атмосферным называется избыточным или манометрическим. Отсчет по шкале избыточных давлений начинается от давления, равного атмосферному. Если из левой и правой частей уравнения (2.3) вычесть величину атмосферного давления p_атм то получим уравнение гидростатики для манометрического давления:

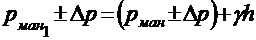(2.4)

По шкале вакуума отсчет давления ведется от p_атм в сторону уменьшения давления (рис.2.1). Вакуумом называется недостаток абсолютного давления до атмосферного.

3. ПРОГРАММА РАБОТЫ.

1. Определить абсолютное давление в четырех точках трубы переменного сечения при изменении давления в расходном бачке.

2. Определить разность давления в каждой точке.

4. ОПИСАНИЕ УСТАНОВКИ.

Рабочий участок гидростенда (рис.1.2) для данной лабораторной работы представляет собой изогнутую трубу переменного сечения. Для определения гидростатического давления в различных сечениях трубы используются пьезометры.

Рис.2.2. Рабочий участок гидростенда.

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Включаем насос, закрываем вентиль 17 (см. описание гидростенда), вентилем 8 устанавливаем максимальное давление в расходном бачке (не более 20 делений манометра).

2. Записываем показания пьезометров h в сечениях 1, 2, 3, 4 и показание манометра n.

3. Выключаем насос.

4. Вентилем 8 уменьшаем давление в расходном бачке и повторяем измерения. Исследования проводятся для четырёх значений давления.

5. Определяем давление по манометру

где n – деление манометра;

– показание барометра (можно принять =₁₀₀₀₀₀_Па₎_.

6. Определяем давление в сечениях трубы

где p₀ – давление на поверхности жидкости (для открытой трубки можно принять равным );

y_i – расстояние от оси трубы до нуля на пьезометрическом щите:

y₁=8 см; y₂=8,5 см; y₃=9 см; y₄=-2 см.

7. Находим разность давления в соответствующих сечениях трубы:

8. Результаты исследований заносим в табл. 2.1. и делаем выводы об их соответствии закону Паскаля.

Таблица 2.1

№ опыта

показания

манометра

Давление манометра,

Па

Показания пьезометров,

Давление в трубе, Па

p_ман

∆p_ман

h₁

h₂

h₃

h₄

p₁

∆р₁

р₂

∆р₂

р₃

∆р₃

р₄

∆р₄

6. КОНТРАЛЬНЫЕ ВОПРОСЫ.

1. В каких случаях применяется основное уравнение гидростатики и закон Паскаля?

2. Дайте определение абсолютного, манометрического, вакуумметрического давления.

3. Каков теоретический предел вакуума?

4. Какое давление будет в четвертом сечении трубы, если показания пьезометрической трубки h=0?

ЛАБОРАТОРНАЯ РАБОТА №3

ОПЫТНАЯ ДЕМОНСТРАЦИЯ УРАВНЕНИЯ БЕРНУЛЛИ.

1. ЦЕЛЬ РАБОТЫ

Экспериментальное исследование закона сохранения энергии (уравнение Бернулли) для потока реальной несжимаемой жидкости в трубе переменного сечения.

2. УРАВНЕНИЕ БЕРНУЛЛИ.

Уравнение Бернулли выражает закон сохранения энергии для потока жидкости. Для любых двух сечений (1-1 и 2-2 на рис.3.1) элементарной струйки реальной несжимаемой жидкости (например, на оси потока) уравнение Бернулли имеет вид

(3.1)

Рис. 3.1. Схема рабочего участка гидростенда.

где gz – удельная энергия положения;

z₁, z₂ – геометрическая высота, измеряемая от плоскости сравнения до элементарной струйки;

- удельная энергия давления;

р₁, р₂ – гидростатическое давление в данной точке;

- удельная кинетическая энергия;

u – скорость потока элементарной струйки в олределенном сечении;

gh_w – удельная суммарная потеря энергия на преодоление сопротивлений между сечениями 1 и 2.

Уравнение (3.1) можно представить в виде

где Е – полная удельная энергия потока в данном сечении.

Зная Е₁ и Е₂, можно определить потерю энергии, затрачиваемую на преодоление сопротивлений между сечениями 1-1 и 2-2:

, (3.2)

При движении жидкости в трубе её энергия теряется на преодоление сопротивления трения по длине и на местные сопротивления

, (3.3)

где gh_m_р – потеря удельной энергии на трение по длине;

gh_м – потеря удельной энергии на местных сопротивлениях.

Так как в реальной жидкости при её движении всегда имеют место потери энергии, то

Е₁>Е₂>Е₃>…>Е_n

Если все члены уравнения (3.1) разделить на ускорение свободного падения g, то получим уравнение Бернулли в форме напоров

, (3.4)

в котором размерность всех членов – линейная.

Уравнение (3.4) можно представить в виде

H₁=H₂+h_w, (3.5)

где Н – полный напор в данном сечении.

Уравнение Бернулли в форме напоров удобно применять для изучения закономерностей изменения удельной энергии потока жидкости по длине трубы.

3. ПРОГРАММА РАБОТЫ.

1. Определить напор Н в трех точках на оси трубы, найти потери напора.

2. Определить скорость потока на оси трубы.

3. Построить графики изменения полного напора Н и гидростатического напора по длине трубы.

4. ОПИСАНИЕ УСТАНОВКИ.

Рабочий участок гидростенда (см. описание гидростенда ГС-3) для данной лабораторной работы представляет собой трубу переменного сечения (рис.3.1). Для измерения статического и полного давлений жидкости в сечениях 1-1, 2-2 и 3-3 установлены пьезометрические трубки и трубки Пито.

Регулирование расхода жидкости в трубе производится вентилем 8 и 18, причем давление в расходном баке, измеряемое образцовым манометром 1, не должно превышать 20 делений манометра.

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Открываем вентиль 18.

2. Включаем насос, медленно открывая вентиль 8, устанавливаем необходимый напор в расходном бачке (20 делений манометра).

3. После того, как выйдут пузырьки воздуха из трубок, запишем показания пьезометров и трубок Пито во всех сечениях.

4. Плавно закрываем вентиль 8, выключаем насос.

5. Определяем потери энергии между сечениями

; .

6. Находим измеренный скоростной напор в каждом сечении

7. Определить скорость потока на оси трубы

8. Результаты исследований записываем в табл.3.1.

9. Строим графики изменения полного напора по длине трубы

и пьезометрического напора

Таблица 3.1

№ сечения	Ордината Z, см	Расстояние между сечениями l, см	Внутренний диаметр трубы d, см	Показания пьезометрической трубки h’’, см	Показания трубки Пито h’, см	Потери напора h_W, см	Скоростной напор h_v, см	Скорость на оси трубы ν, см/с	Измеренный полный напор H, см	Измеренный пьезометрический напор H_p, см
1		37	1.4
2		37	2.8
2		37	2.8
3		37	1.2

6. КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Объясните физическую сущность каждого из членов уравнения Бернулли для реального потока жидкости.

2. Что такое удельная энергия, и какова её размерность.

3. При каком давлении жидкости полный и пьезометрический напоры изменяются по длине на одну и ту же величину?

4. В чем отличие уравнения Бернулли для элементарной струйки и для потока жидкости?

5. В каком случае уравнение Бернулли превращается в основное уравнение гидростатики?

6. Какое давление будет в напорном потоке, если пьезометрическая линия проходит ниже его геометрической оси?

ЛАБОРАТОРНАЯ РАБОТА № 4.

ИССЛЕДОВАНИЕ РЕЖИМОВ ДВИЖЕНИЯ ЖИДКОСТИ.

1. ЦЕЛЬ РАБОТЫ.

Визуальное наблюдение ламинарного и турбулентного режимов движения жидкости. Определение значений числа Рейнольдса, соответствующих ламинарному и турбулентному режимам течения жидкости.

2. ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ.

При движении жидкости в трубопроводе могут возникать два режима течения, которые значительно отличаются один от другого.

При ламинарном режиме движения отдельные частицы жидкости перемещаются в трубе параллельно её стенкам, поперечные перемещения при этом отсутствуют. Если мы в такой поток будем подавать через тонкую трубку краску, то краска будет перемещаться тонкой струйкой, параллельно стенкам трубы, не смешиваясь с остальным потоком воды (рис.4.1а.).

а) б)

Рис.4.1. Характер движения воды в трубе:

а) ламинарный режим; б) турбулентный режим.

Турбулентный режим движения характеризуется наличием поперечных перемещений частиц жидкости по всему потоку, которые движутся по произвольным траекториям. Имеют место также пульсации скоростей и давления в каждой точке потока. При введении краски в такой поток отдельные частицы краски распространяются по всему объему трубы, равномерно окрашивая всю массу жидкости (рис.4.1б).

Режим движения жидкости зависит от следующих параметров потока: средней скорости движения u, внутреннего диаметра трубы d и кинематического коэффициента вязкости n.

Критерием, определяющим режим движения жидкости, является число Рейнольдса

. (4.1)

Смена режима движения жидкости с ламинарного на турбулентный происходит при числах Рейнольдса от 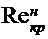≤ 2000 (нижний критический предел) до ≥ 10000 (верхний критический предел). При значениях числа Рейнольдса в пределах 2000 < Re < 10000 могут наблюдаться и ламинарный, и турбулентный режимы, которые будут неустойчивы. Область неустойчивого течения называется переходной зоной.

На практике для упрощения расчётов принимают, что при Re < 2320 – режим течения ламинарный; при Re ≥ 2320 – турбулентный.

Зная скорость движения жидкости, её вязкость и диаметр трубы, можно найти число Re, и сравнив его с Re_кр, определить режим течения жидкости.

Отличие турбулентного потока от ламинарного приведено в табл.4.1.

На практике встречается и ламинарный, и турбулентный режимы движения жидкости. Ламинарный режим чаще имеет место тогда, когда по трубам движутся вязкие жидкости (масла), турбулентный – при течении маловязких жидкостей (вода, бензин, керосин и др.).

3. ПРОГРАММА РАБОТЫ.

1. Установить последовательно ламинарный и турбулентный режимы движения жидкости в трубе.

2. Определить число Рейнольдса для каждого режима движения.

3. Измерить максимальную скорость потока на оси трубы и сравнить её значение со средней скоростью.

Таблица 4.1

Параметры потока

Ламинарный режим

Турбулентный режим

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: