Основные понятия
Обыкновенным дифференциальным уравнением (ДУ) называется соотношение (уравнение), связывающее независимую переменную 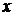 , искомую функцию
, искомую функцию  и ее производные
и ее производные  (дифференциалы). Это уравнение имеет следующий общий вид:
(дифференциалы). Это уравнение имеет следующий общий вид:
 .
.
Порядкомдифференциального уравнения называется порядок высшей производной (дифференциала), входящей в ДУ.
Например,  – обыкновенное ДУ первого порядка, а
– обыкновенное ДУ первого порядка, а  – обыкновенное ДУ третьего порядка.
– обыкновенное ДУ третьего порядка.
Решением дифференциального уравнения называется функция  , которая при подстановке в уравнение обращает его в тождество. График решения называется интегральной кривой уравнения. Соотношение
, которая при подстановке в уравнение обращает его в тождество. График решения называется интегральной кривой уравнения. Соотношение  называется интегралом уравнения.
называется интегралом уравнения.
Общим решением (общим интегралом) дифференциального уравнения является решение (интеграл), которое содержит n независимых произвольных констант, где n – порядок уравнения.
Задача Коши для дифференциального уравнения – задание дополнительно начальных условий вида:  .
.
Частным решением (частным интегралом), удовлетворяющим заданным начальным условиям (решением задачи Коши), является такое решение дифференциального уравнения, полученное из общего, которое удовлетворяет еще дополнительным условиям задачи Коши.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка в общем случае можно записать в виде  .
.
Если уравнение можно разрешить относительно  , то его записывают в виде
, то его записывают в виде  .
.
Уравнения с разделяющимися переменными
Определение. Уравнение вида  (или в дифференциальной форме
(или в дифференциальной форме  ) называется уравнением с разделяющимися переменными.
) называется уравнением с разделяющимися переменными.
В частности, функции 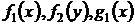 или
или  могут быть постоянными, т.е. равны Const.
могут быть постоянными, т.е. равны Const.
Способ решения. Для решения уравнений с разделяющимися переменными нужно разделить переменные, т.е. при dx оставить функцию, зависящую только от x, а при dy – только от y, и затем проинтегрировать обе части уравнения.
Пример. Найти общий интеграл уравнения  .
.
Решение:
Перенесем слагаемое, не содержащее производную, вправо:  . Запишем производную
. Запишем производную  в виде
в виде 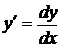 . Тогда дифференциальное уравнение примет вид
. Тогда дифференциальное уравнение примет вид
 .
.
Разделим переменные:
 .
.
Интегрируем обе части уравнения:
 ,
,  .
.
Примечание: Так как в левой части уравнения после интегрирования возник логарифм, то константа С добавлена в виде 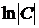 для более удобного дальнейшего потенциирования.
для более удобного дальнейшего потенциирования.
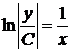 ,
,  ,
,  – общее решение исходного уравнения.
– общее решение исходного уравнения.
Сделаем проверку:
Найдем производную общего решения 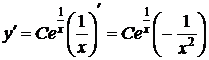 . Подставим
. Подставим  и
и  в исходное уравнение:
в исходное уравнение:  ,
,  , что и требовалось доказать. Следовательно, решение уравнения найдено верно.
, что и требовалось доказать. Следовательно, решение уравнения найдено верно.
Ответ: Общее решение:  .
.
Однородные уравнения
Определение. Уравнение вида  (
( ), где функции
), где функции 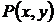 и
и  – однородные функции одинакового порядка, называется однородным дифференциальным уравнением первого порядка.
– однородные функции одинакового порядка, называется однородным дифференциальным уравнением первого порядка.
Определение. Функция  называется однородной функцией n-го порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель
называется однородной функцией n-го порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель 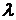 вся функция умножится на
вся функция умножится на 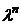 , т.е.
, т.е.
 .
.
Например, функция 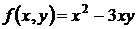 есть однородная функция второго порядка, поскольку
есть однородная функция второго порядка, поскольку
 .
.
Способ решения. Однородное уравнение сводится к уравнению с разделяющимися переменными при помощи замены переменной (подстановки)
 или, что то же самое,
или, что то же самое,  .
.
Подставив в однородное уравнение  и
и  (если уравнение в дифференциальной форме, то
(если уравнение в дифференциальной форме, то  ), получим уравнение с разделяющимися переменными. Найдя его общее решение, следует заменить в нем
), получим уравнение с разделяющимися переменными. Найдя его общее решение, следует заменить в нем  на
на  . Получим общее решение (интеграл) исходного уравнения.
. Получим общее решение (интеграл) исходного уравнения.
Пример. Решить уравнение  .
.
Решение:
Перенесем все слагаемые вправо:  . Проверим, является ли это уравнение однородным.
. Проверим, является ли это уравнение однородным.
Для этого проверим, являются ли функции 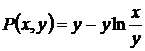 и
и  однородными функциями одинакового порядка:
однородными функциями одинакового порядка:
 ,
,
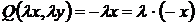 .
.
Действительно, функции P и Q – однородные функции первого порядка, следовательно, исходное уравнение однородное.
Положим  и
и  . Подставляем в исходное уравнение:
. Подставляем в исходное уравнение:
 ,
,  ,
,  ,
,
 ,
,  – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
Перенесем слагаемое, не содержащее производную, вправо:  . Запишем производную
. Запишем производную  в виде
в виде
 .
.
Тогда дифференциальное уравнение примет вид
 .
.
Разделим переменные:
 .
.
Интегрируем обе части уравнения:
 .
.
 .
.
В итоге, имеем
 ,
,  ,
,  ,
,  .
.
Подставив вместо  , окончательно получим общий интеграл исходного уравнения
, окончательно получим общий интеграл исходного уравнения  , или общее решение
, или общее решение 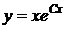 .
.
Ответ: Общее решение: 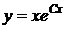 .
.
Линейные уравнения
Определение. Дифференциальное уравнение вида  (или
(или  ) называется линейным дифференциальным уравнением первого порядка.
) называется линейным дифференциальным уравнением первого порядка.
В частности, функции 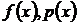 или
или 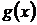 могут быть равны Const. Особенность этого уравнения: искомая функция
могут быть равны Const. Особенность этого уравнения: искомая функция  и ее производная
и ее производная  входят в уравнение в первой степени, не перемножаясь между собой.
входят в уравнение в первой степени, не перемножаясь между собой.
При  уравнение называется линейным однородным дифференциальным уравнением первого порядка.
уравнение называется линейным однородным дифференциальным уравнением первого порядка.
Способ решения. Решать уравнение можно с помощью подстановки 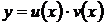 (метод Бернулли) или методом вариации произвольной постоянной (метод Лагранжа). Покажем оба метода на примере.
(метод Бернулли) или методом вариации произвольной постоянной (метод Лагранжа). Покажем оба метода на примере.
Пример. Решить уравнение  .
.
Решение:
 2018-02-13
2018-02-13 5607
5607