Теор: Пусть G ограничена жордановой спрямляемой кривой Т и 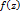 -ф-ции, голоморфной в G и непрерывной в
-ф-ции, голоморфной в G и непрерывной в  , тогда
, тогда 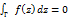
Док-во: проведем, при доп предп, что каждый луч выходит из точки  , пересекая Г только в одной точке и что Г состоит из конечного числа гладких дуг. РИС
, пересекая Г только в одной точке и что Г состоит из конечного числа гладких дуг. РИС
Пусть  ,
,  –ур-ние крив Г,
–ур-ние крив Г,  - по предположению имеет кусочно-непрер произв
- по предположению имеет кусочно-непрер произв 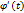 , пусть
, пусть 
Рассмотрим замкнутую кривую  ,
, 
По теор Коши:  =
=  , сл-но
, сл-но

Ф-ция f(z)-равномерно непрер в замкнутой области  , поэтому
, поэтому  , что при
, что при  ,
,  имеем
имеем 
Положим  ,
,  ,
,  ,
,  , тогда при
, тогда при  имеем
имеем  (
( , поэтому при указанном
, поэтому при указанном 
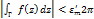
Интегральная формула Коши. Теорема о среднем
. Теор: Пусть G-односвязанная область, ограниченная Жардановой спрямляемой кривой Г. f(z)-голоморфная функция замкнутой области G, тогда для  точки
точки  справедлива формула:
справедлива формула:  (1) (кривая Г проходится в положительном направлении)
(1) (кривая Г проходится в положительном направлении)
Док-во: фиксир.  . Пусть
. Пусть 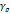 - окружность радиуса ρ с центром в точке z, целиком лежащей в G. РИС. Рассмотрим так же функцию
- окружность радиуса ρ с центром в точке z, целиком лежащей в G. РИС. Рассмотрим так же функцию  (2). Эта функция является голоморфной в области, лежащей между контурами Г и
(2). Эта функция является голоморфной в области, лежащей между контурами Г и  , включая контура.
, включая контура.
На основании теоремы Коши  (3), это рав-во показывает, что
(3), это рав-во показывает, что  .
.
Из рав-ва 2 =>, что  , когда
, когда  . Положив
. Положив  , получим непрерывно замкнутую область
, получим непрерывно замкнутую область  функции
функции  . Сл-но
. Сл-но 
 , что
, что 
 . Откуда получаем:
. Откуда получаем:  , откуда следует, что
, откуда следует, что  , т.к
, т.к  сколь угодно мало, а знач
сколь угодно мало, а знач  постоянное число.
постоянное число.
Рав-во 3 примет вид  ,
,  или
или 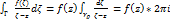
Опред: мн-л  наз интегралом Коши.
наз интегралом Коши.
Во всякой т. z не принадлеж  ин-л Коши по теор Коши =0.
ин-л Коши по теор Коши =0.
Поскольку ф  в этом случае является голоморфной в
в этом случае является голоморфной в 
 РИС
РИС
 2018-02-13
2018-02-13 198
198








